4.1. Transforming Sequences with Comprehensions¶

4.1.1. List Comprehensions¶

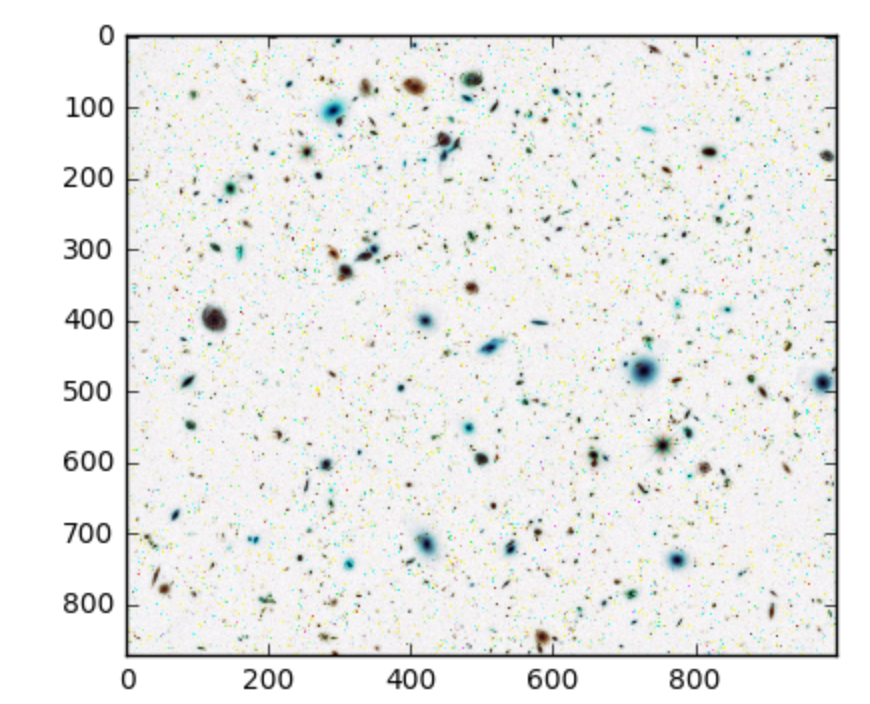
Suppose that we wish to create a list from a sequence of values based on some selection criteria. An easy way to do this type of processing in Python is to use a list comprehension. List comprehensions are concise ways to create lists. The general syntax is:

[<expression> for <item> in <sequence> if  <condition>]

where the if clause is optional. For example,

In [1]: mylist = [1,2,3,4,5]

In [2]: yourlist = [item ** 2 for item in mylist]

In [3]: yourlist
Out[3]: [1, 4, 9, 16, 25]

The expression describes each element of the list that is being built. The for clause iterates through each item in a sequence. The items are filtered by the if clause if there is one. In the example above, the for statement lets item take on all the values in the list mylist one after the other. Each item is then squared before it is added to the list that is being built. The result is a list of squares of the values in mylist.

The three parts of a comprehension are the output expression, the description of the sequence, and the (optional) predicate. This image is copied from the open source Python 3 Patterns, Recipes and Idioms book and is shared under the Creative Commons Attribution-Share Alike 3.0 license.

The built-in range Python function is a useful tool for generating a sequence of numbers. The sequence provided by range always starts with 0. If you ask for range(4), then you will get 4 values starting with 0. In other words, 0, 1, 2, and finally 3. Notice that 4 is not included since we started with 0. Likewise, range(10) provides 10 values, 0 through 9.

In [4]: [ i for i in range(4)]
Out[4]: [0, 1, 2, 3]

In [5]: [x for x in range(10)]
Out[5]: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

The range function is actually a very powerful function when it comes to creating sequences of integers. It can take one, two, or three parameters. We have seen the simplest case of one parameter such as range(4) which creates [0, 1, 2, 3]. But what if we really want to have the sequence [1, 2, 3, 4]? We can do this by using a two parameter version of range where the first parameter is the starting point and the second parameter is the ending point. The evaluation of range(1,5) produces the desired sequence. What happened to the 5? In this case we interpret the parameters of the range function to mean range(start,stop+1).

Here are a three examples for you to considered.

In [6]: [i for i in range(4)]
Out[6]: [0, 1, 2, 3]

In [7]: [x for x in range(1, 10)]
Out[7]: [1, 2, 3, 4, 5, 6, 7, 8, 9]

In [8]: [item for item in range(1,10,2)]
Out[8]: [1, 3, 5, 7, 9]

Notice that the last call to range added the third parameter, which represents the step size. In this case, every item is 2 more than the last item. Making a list that counts down from some starting number can be accomplished using a negative step size.

In [9]: [ i for i in range(10, 0, -1)]
Out[9]: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]

Check your understanding

rec-5-55: In the command range(3, 10, 2), what does the second argument (10) specify?
• (A) Range should generate a list that stops at 9 (including 9).
• Range will generate the list [3, 5, 7, 9].
• (B) Range should generate a list that starts at 10 (including 10).
• The first argument (3) tells range what number to start at.
• (C) Range should generate a list starting at 3 that stops at 10 (including 10).
• Range will always stop at the number before (not including) the specified ending point for the list.
• (D) Range should generate a list using every 10th number between the start and the stopping number.
• The third argument (2) tells range how many numbers to skip between each element in the list.

rec-5-56: What command correctly generates the list [2, 5, 8]?
• (A) range(2, 5, 8)
• This command generates the list [2] because the first number (2) tells range where to start, the second number tells range where to end (5, not inclusive) and the third number tells range how many numbers to skip between elements (8). Since 10>= 8, there is only one number in this list.
• (B) range(2, 8, 3)
• This command generates the list [2, 5] because 8 is not less than 8 (the specified ending number).
• (C) range(2, 10, 3)
• The first number is the starting point, the second is the maximum allowed, and the third is the amount to increment by.
• (D) range(8, 1, -3)
• This command generates the list [8, 5, 3] because it starts at 8, ends at (or above 1), and skips every third number going down.

rec-5-57: What happens if you give range only one argument? For example: range(4)
• (A) It will generate a list starting at 0, with every number included up to but not including the argument it was passed.
• Yes, if you only give one number to range it starts with 0 and ends before the number specified incrementing by 1.
• (B) It will generate a list starting at 1, with every number up to but not including the argument it was passed.
• Range starts at 0 unless otherwise specified.
• (C) It will generate a list starting at 1, with every number including the argument it was passed.
• Range starts at 0 unless otherwise specified, and never includes its ending element (which is the argument it was passed).
• (D) It will cause an error: range always takes exactly 3 arguments.
• If range is passed only one argument, it interprets that argument as the end of the list (not inclusive).

One final note about the range function in python: it is lazy! Notice that trying to evaluate this function by itself doesn’t return the list. Instead, it returns a generator object that will wait as long as possible to generate this list.

In [10]: range(5)
Out[10]: range(0, 5)

We have a number of methods for forcing range to complete the process including comprehensions and the list conversion function.

In [11]: list(range(5))
Out[11]: [0, 1, 2, 3, 4]

An alternative method for generating odd values involves using a Boolean function to filter items out of our list using the optional if clause. For example, let’s compute the cube root for all odd values less than 10.

In [12]: is_odd = lambda x: x % 2 == 1

In [13]: cube_root = lambda x: x**(1/3)

In [14]: [cube_root(x) for x in range(10) if is_odd(x)]
Out[14]: 
[1.0,
 1.4422495703074083,
 1.7099759466766968,
 1.912931182772389,
 2.080083823051904]

Why might we want to use this version of the comprehension? Here we are using two explicit abstractions to describe the intent of our code. This should make it easier for someone that later reads through the code to understand the meaning of this construction, i.e. that we are taking the cube root of odd numbers up to 10.

Check your understanding

rec-5-58: What is printed by the following statements?

alist = [4,2,8,6,5]
blist = [num*2 for num in alist if num%2==1]
print(blist)

• (A) [4,2,8,6,5]
• Items from alist are doubled before being placed in blist.
• (B) [8,4,16,12,10]
• Not all the items in alist are to be included in blist. Look at the if clause.
• (C) 10
• The result needs to be a list.
• (D) [10].
• Yes, 5 is the only odd number in alist. It is doubled before being placed in blist.

4.1.2. List Comprehensions for Two Dimensional Data¶

Two dimensional (2D) data is data that can be displayed in a table. An examples of two dimensional data include matrices and images. We can use list comprehensions to transform and filter 2D data by embedding one list comprehension in another.

Consider the following matrix of integers.

One method for representing this matrix in Python is with a list of lists.

In [15]: mat = [[1,2,3],[4,5,6],[7,8,9]]

In [16]: mat
Out[16]: [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

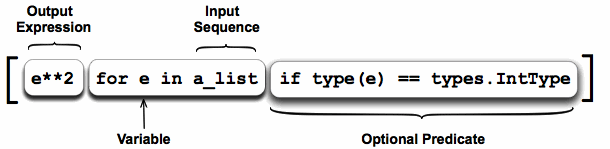
To write a comprehension that transforms 2D data into another 2D list, we embed a comprehension inside a comprehension.

A 2D comprehension consists of a list comprehension inside another comprehension. The outer sequence consists of all rows of the matrix and the inner sequence consists of elements from each row. The inner comprehension can be thought of as representing each of the new rows in the resulting matrix.

For example, the following code will generate a new matrix that contains the square of each value from the first matrix.

In [17]: new_mat = [[e**2 for e in row] for row in mat]

In [18]: new_mat
Out[18]: [[1, 4, 9], [16, 25, 36], [49, 64, 81]]

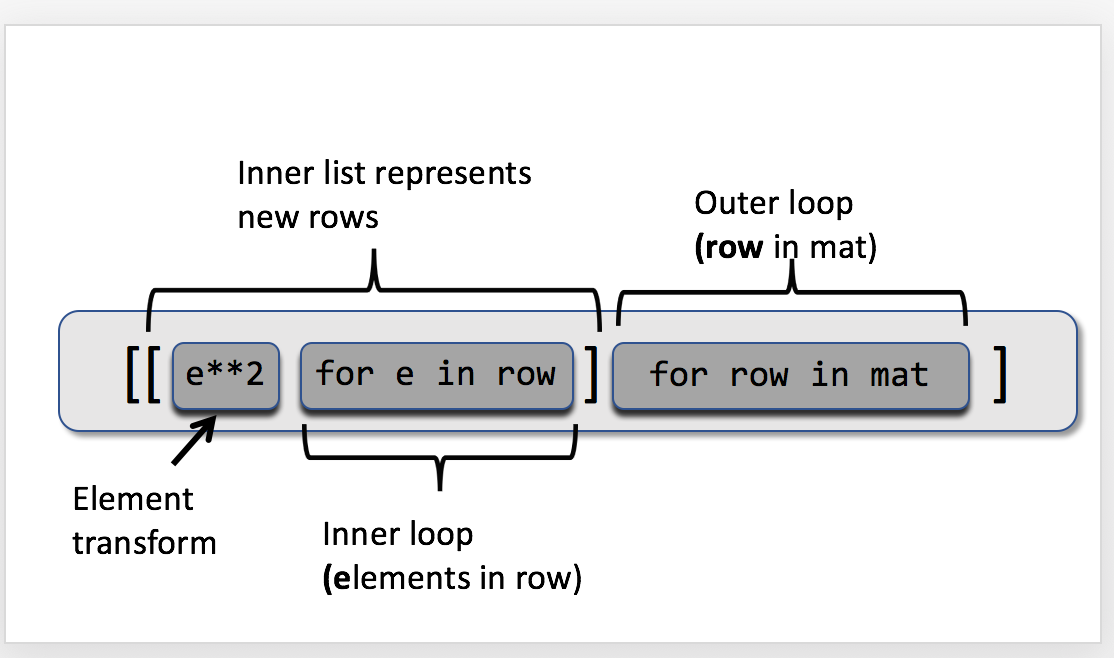
For this example, we will transform an image by replacing all of the black pixels with white pixels. Recall that an image from skimage is stored as a 3D array of RGB values, but can be iterated over as a 2D matrix of tuples of 3 values. Consider the following code,

from skimage import data
import matplotlib.pylab as plt
import numpy as np
%matplotlib inline
hub = data.hubble_deep_field()
plt.imshow(hub)

which displays the following image.

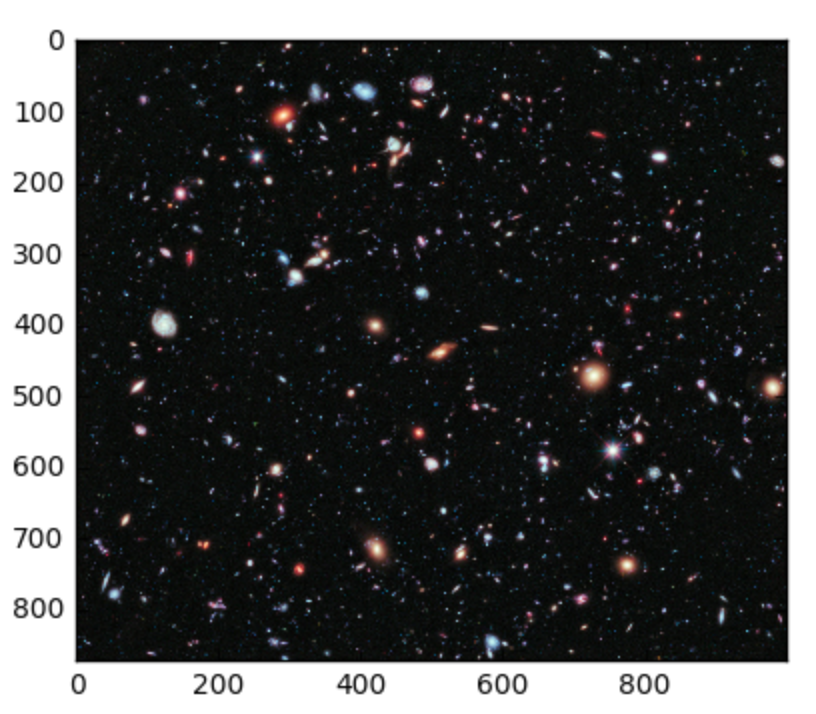
The RGB code for (pure) black is (0,0,0). The following code splits the task into three parts. First, the function is_black checks that each color is 0. Next, the function black_to_white switches black to white (rgb(255,255,255)), but otherwise leaves the color as is. Finally, a 2D comprehension is used to make a new image matrix or tuples. Note that this array needs to be converted to a numpy array.

# Black RGB is (0, 0, 0), we check that all colors == 0
is_black = lambda t: all([col == 0 for col in t])

# Replace black (0,0,0) with white (255, 255, 255) else leave it alone
black_to_white = lambda t: (255,255,255) if is_black(t) else t

#apply black_to_white to each RGB tuple
new_img = np.array([[black_to_white(tup) for tup in row] for row in hub])
plt.imshow(new_img)

The resulting image is shown below.