7.3. Three General Tasks¶

7.3.1. Map¶

A map is the operation of applying or mapping a function to each element of a list. An example would be squaring all the elements in a list.

In [1]: L = [1,2,3,4,5]

In [2]: sqr = lambda x: x**2

In [3]: sqr_L = [sqr(x) for x in L]

In [4]: sqr_L
Out[4]: [1, 4, 9, 16, 25]

In fact, the form of applying a map with a list comprehension will always have the following form shown below for some function f.

General Form of a map

mapped_L = [f(x) for x in L]

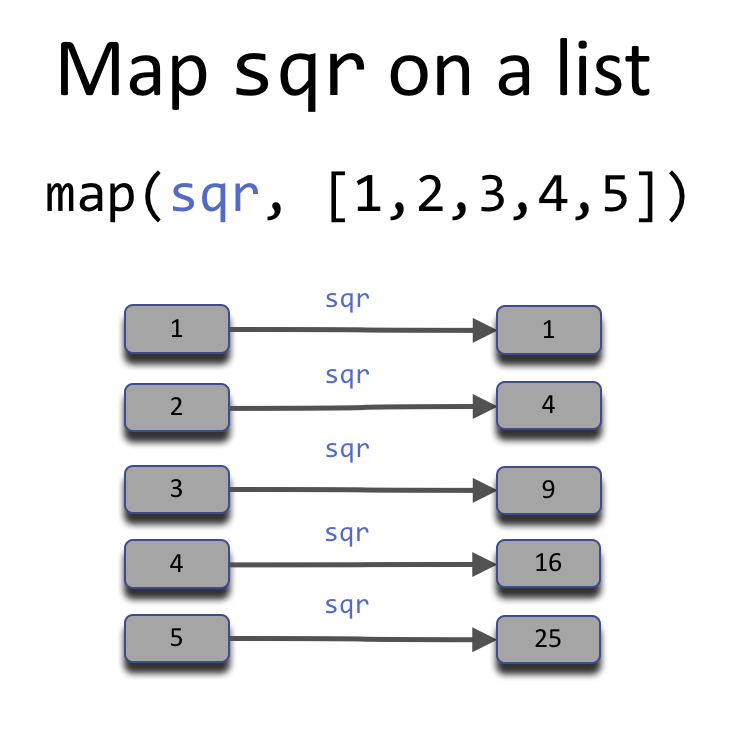
The function map applies sqr (first argument) to each element of the list (second argument).

Since this is a common functional pattern, we should construct a general abstraction. For this expression, we would want to be able to change the function f being mapped and the list L. The following definition gives an abstraction for map (titled my_map to avoid shadowing the built-in map).

In [5]: my_map = lambda func, L: [func(item) for item in L]

In [6]: my_map(lambda x: x**2, range(5))
Out[6]: [0, 1, 4, 9, 16]

In the above example, the first argument of my_map is the function (lambda expression) that will be applied to each element and the second argument is the sequence to be processed. Python has a built-in function map that generalizes this process.

In [7]: out = map(lambda x: x**2, range(5))

In [8]: out
Out[8]: <map at 0x10fdb8390>

In [9]: type(out)
Out[9]: map

In [10]: list(out)
Out[10]: [0, 1, 4, 9, 16]

In [11]: out
Out[11]: <map at 0x10fdb8390>

# out has been processed and is now empty
In [12]: [x for x in out]
Out[12]: []

# We need to reinitialize out to process a second time.
In [13]: out = map(lambda x: x**2, range(5))

In [14]: [x for x in out]
Out[14]: [0, 1, 4, 9, 16]

Like the range function, map is lazy and must be forced to complete evaluation using the list conversion function or another list comprehension. It should also be noted that a map can only be processed once. If we want to process a map a second time, it will need to be re-initialized as shown above.

Check your understanding

exceptions-4-8: What will out evaluate to for the following code?

has_vowel = lambda L: any([True for ch in L if ch.lower() in 'aeiou'])
out = map(has_vowel, ['a', 'b', 'c'])

• (A) A lazy object
• The built-in map function is lazy and will return a generator object unless completion is forced by list/comprehension/reduce
• (B) [True, False, False]
• The built-in map function is lazy and will return a generator object unless completion is forced by list/comprehension/reduce
• (C) ['a']
• The built-in map function is lazy and will return a generator object unless completion is forced by list/comprehension/reduce
• (D) Error, you can't use a function as an argument for another function.
• Functions are "first class citizens" in Python, meaning they can be used in the same way as any other piece of data

exceptions-4-9: What will out evaluate to for the following code?

has_vowel = lambda L: any([True for ch in L if ch.lower() in 'aeiou'])
out = list(map(has_vowel, ['a', 'b', 'c']))

• (A) A lazy object
• Applying the list conversion function to map will force completion of the lazy generator object returned by map.
• (B) [True, False, False]
• Map will apply has_vowel to each letter in the list, keeping the resulting Boolean value.
• (C) ['a']
• This would be the result of filter. Map will apply has_vowel to each letter in the list, keeping the resulting Boolean value.
• (D) Error, you can't use a function as an argument for another function.
• Functions are "first class citizens" in Python, meaning they can be used in the same way as any other piece of data

exceptions-4-10: Which of the following functions can be used to replace has_vowel?

has_vowel = lambda L: any([True for ch in L if ch.lower() in 'aeiou'])

• (A) lambda L: any(map(lambda ch: ch.lower() in 'aeiou', L))
• Map will check if each character is a vowel and any will return True if there is at least on vowel in the list.
• (B) lambda L: all(map(lambda ch: ch.lower() in 'aeiou', L))
• Map will check if each character is a vowel but all would only return True if ALL of the characters in the list are vowels.

7.3.2. Filter¶

A filter is the operation of filtering the list to only include values that fit some condition. For example, we would filter out all of the odd number from a list of numbers.

In [15]: L = [1,2,3,4,5]

In [16]: is_odd = lambda x: x % 2 == 1

In [17]: odd_L = [x for x in L if is_odd(x)]

In [18]: odd_L
Out[18]: [1, 3, 5]

Once again, the basic form of a filter is easy to express in the form of a list comprehension. Let predicate be a Boolean function that checks the condition by which we filter. Then a filter operation can be expressed as follows.

General form of a filter

filtered_L = [x for x in L if predicate(x)]

When applying filter with is_odd (first argument) to the list [1,2,3,4,5] (second argument), all of the values where is_odd returns True are retained.

As with map, we can easily create an abstraction of this pattern. In this case, we want to be able to change the predicate function as well as the list being processed.

In [19]: my_filter = lambda pred, L: [x for x in L if pred(x)]

In [20]: my_filter(lambda x: x % 2 == 1, range(1,6))
Out[20]: [1, 3, 5]

my_filter will iterate though all of the elements of the second argument range(1,6), applying lambda x: x % 2 == 1 and only keeping the values which return true. Python also comes with a built-in, lazy implementation of filter. As with map, we need to force completion of this process using the list conversion function or another list comprehension and the filter object will be empty after being processed.

In [21]: out = filter(lambda x: x % 2 == 1, range(1,6))

In [22]: out
Out[22]: <filter at 0x10fc816a0>

In [23]: type(out)
Out[23]: filter

In [24]: list(out)
Out[24]: [1, 3, 5]

Check your understanding

exceptions-4-11: What will out evaluate to for the following code?

has_vowel = lambda L: any([True for ch in L if ch.lower() in 'aeiou'])
out = filter(has_vowel, ['a', 'b', 'c'])

• (A) A lazy object
• The built-in filter function is lazy and will return a generator object unless completion is forced by list/comprehension/reduce
• (B) [True, False, False]
• The built-in filter function is lazy and will return a generator object unless completion is forced by list/comprehension/reduce
• (C) ['a']
• The built-in filter function is lazy and will return a generator object unless completion is forced by list/comprehension/reduce
• (D) Error, you can't use a function as an argument for another function.
• Functions are "first class citizens" in Python, meaning they can be used in the same way as any other piece of data

exceptions-4-12: What will out evaluate to for the following code?

has_vowel = lambda L: any([True for ch in L if ch.lower() in 'aeiou'])
out = list(filter(has_vowel, ['a', 'b', 'c']))

• (A) A lazy object
• Applying the list conversion function to map will force completion of the lazy generator object returned by map.
• (B) [True, False, False]
• This would be the result of map. Filter will only keep values for which has_vowel is True.
• (C) ['a']
• Filter will only keep values for which has_vowel is True.
• (D) Error, you can't use a function as an argument for another function.
• Functions are "first class citizens" in Python, meaning they can be used in the same way as any other piece of data

7.3.3. Reduce¶

The third general operation performed on lists is a reduction, which reduces a list to a value. Simple reductions can be performed using a list comprehension in combination with one of Python’s built-in reducers like sum, len, any, all, max and min. For example, we can count the number of odd values in a list by combining a filter with the len reducer function.

In [25]: L = [1,2,3,4,5]

In [26]: is_odd = lambda x: x % 2 == 1

In [27]: num_odd = len([x for x in L if is_odd(x)])

In [28]: num_odd
Out[28]: 3

This action reduced the list to a value, namely the number of odd entries. Furthermore, this example illustrates how we can combine these basic operations of map, filter and reduce to complete a task. In this case we first filter out the odd values and then reduce that list to the length of the list.

While map and filter are easily represented using list comprehensions, we have had to rely on Python built-in functions to reduce lists to values. In general, we will need to look for a more general solution to these problems and the standard functional approach is through recursion.

Let’s look at the imperative solution to a few reduction problems and see if we can see a pattern.

Problem 1 - Compute the sum of all the numbers in a list

In [29]: my_list = [1,2,3,4,5]

In [30]: def sum_list(L):
   ....:     acc = 0
   ....:     for item in L:
   ....:         acc = acc + item
   ....:     return acc
   ....: 

In [31]: sum_list(my_list)
Out[31]: 15

Problem 2 - Join all the strings in a list into one string

In [32]: my_strings = ["a", "b", "c"]

In [33]: def join_strings(L):
   ....:     acc = L[0]
   ....:     for item in L[1:]:
   ....:         acc = acc + item
   ....:     return acc
   ....: 

In [34]: join_strings(my_strings)
Out[34]: 'abc'

Problem 3 - Take a list of numbers and return a list of cumulative sums

In [35]: my_numbers = [1,2,3,4,5]

In [36]: def cumult_sum(L):
   ....:     acc = [L[0]]
   ....:     for item in L[1:]:
   ....:         acc = acc + [acc[-1] + item]
   ....:     return acc
   ....: 

In [37]: cumult_sum(my_numbers)
Out[37]: [1, 3, 6, 10, 15]

First note that join_strings uses the first entry in the sequence as the initial value and iterates over the rest of the sequence. This approach will be valid with many reduction problems, and will make a nice default for our initial value.

Each of the solutions shown above are examples of the accumulator pattern. In each case, the variable acc is set to some initial value and then updated as we iterate though each value. Also note how very similar the shape of the code is in these examples. A little refactoring will make this very clear. We will modify the code in two ways. First, the initial value will be made a parameter of each function. Second, we will define and use a separate function to update the accumulator.

Problem 1 - Compute the sum of all the numbers in a list

In [38]: my_list = [1,2,3,4,5]

In [39]: def update(acc, item):
   ....:     return acc + item
   ....: 

In [40]: def sum_list(L,init):
   ....:     acc = init
   ....:     for item in L:
   ....:         acc = update(acc, item)
   ....:     return acc
   ....: 

In [41]: sum_list(my_list, 0)
Out[41]: 15

Problem 2 - Join all the strings in a list into one string

In [42]: my_strings = ["a", "b", "c"]

In [43]: def update(acc, item):
   ....:     return acc + item
   ....: 

In [44]: def join_strings(L, init):
   ....:     acc = init
   ....:     for item in L:
   ....:         acc = update(acc, item)
   ....:     return acc
   ....: 

In [45]: join_strings(my_strings[1:], my_strings[0])
Out[45]: 'abc'

Problem 3 - Take a list of numbers and return a list of cumulative sums

In [46]: my_numbers = [1,2,3,4,5]

In [47]: def update(acc, item):
   ....:     return acc + [acc[-1] + item]
   ....: 

In [48]: def cumult_sum(L, init):
   ....:     acc = init
   ....:     for item in L:
   ....:         acc = update(acc, item)
   ....:     return acc
   ....: 

In [49]: cumult_sum(my_numbers[1:],[my_list[0]])
Out[49]: [1, 3, 6, 10, 15]

These three functions look to be identical, but they are all referencing a different (globally defined) update function. Recall that all Python data are object, including functions. The final modification we will make, it adding a parameter for the update function, allowing us to answer all three problems with one function. In Python and LISP, this function is know as reduce. In other languages, such as Haskell, this function is called foldl for fold from the left. In the process of making this last refactor, we will also set up a default value of init, making sure to iterate through the rest of the list if using the default.

In [50]: my_list = [1,2,3,4,5]

In [51]: my_strings = ["a", "b", "c"]

In [52]: my_numbers = [1,2,3,4,5]

In [53]: def reduce(function, L,init=None):
   ....:     if init:
   ....:         acc = init
   ....:     else:
   ....:         acc = L[0]
   ....:         L = L[1:]
   ....:     for item in L:
   ....:         try:
   ....:             acc = function(acc, item)
   ....:         except:
   ....:             print(acc, init, item)
   ....:     return acc
   ....: 

In [54]: list_sum = reduce(lambda a, i: a+i, my_list)

In [55]: list_sum
Out[55]: 15

In [56]: my_str = reduce(lambda a, i: a + i, my_strings)

In [57]: my_str
Out[57]: 'abc'

In [58]: csum = reduce(lambda a, i: a + [a[-1] + i], my_numbers[1:], [my_numbers[0]])

In [59]: csum
Out[59]: [1, 3, 6, 10, 15]

In reality, we didn’t need to write this function, as it is provided in the standard functools library.

In [60]: from functools import reduce

In [61]: reduce(lambda a, i: a + i**2, [1,2,3,4,5], 0)
Out[61]: 55

It will probably take a while to get used to reading a call to reduce. You should think of the first argument as the accumulator update function. The reduce will keep updating the accumulator as it processes the list. Let’s step through the process item by item to illustrate.

First, to make iterating through L one item at a time, we construct and iterator for L using the iter function called iter_L. Then the next element of L is acquired by applying next to iter_L. We start by setting the accumulator acc to the initial value. Then acc is updated using the current value of the accumulator and the next element in the list.

In [62]: L = [1,2,3,4]

In [63]: iter_L = iter(L)

In [64]: init = 0

In [65]: f = lambda a, i: a + i**2

In [66]: acc = 0

In [67]: current_item = next(iter_L)

In [68]: current_item
Out[68]: 1

In [69]: acc = f(acc, current_item)

In [70]: acc
Out[70]: 1

This process is continued until all of the elements of the list have been processed (from left to right).

In [71]: current_item = next(iter_L)

In [72]: current_item
Out[72]: 2

In [73]: acc = f(acc, current_item)

In [74]: acc
Out[74]: 5

In [75]: current_item = next(iter_L)

In [76]: current_item
Out[76]: 3

In [77]: acc = f(acc, current_item)

In [78]: acc
Out[78]: 14

In [79]: current_item = next(iter_L)

In [80]: current_item
Out[80]: 4

In [81]: acc = f(acc, current_item)

In [82]: acc
Out[82]: 30

With some practice, you will be able to think about reducing a list to a value using this high level abstraction (and will (almost) never need to write the accumulator pattern again!)

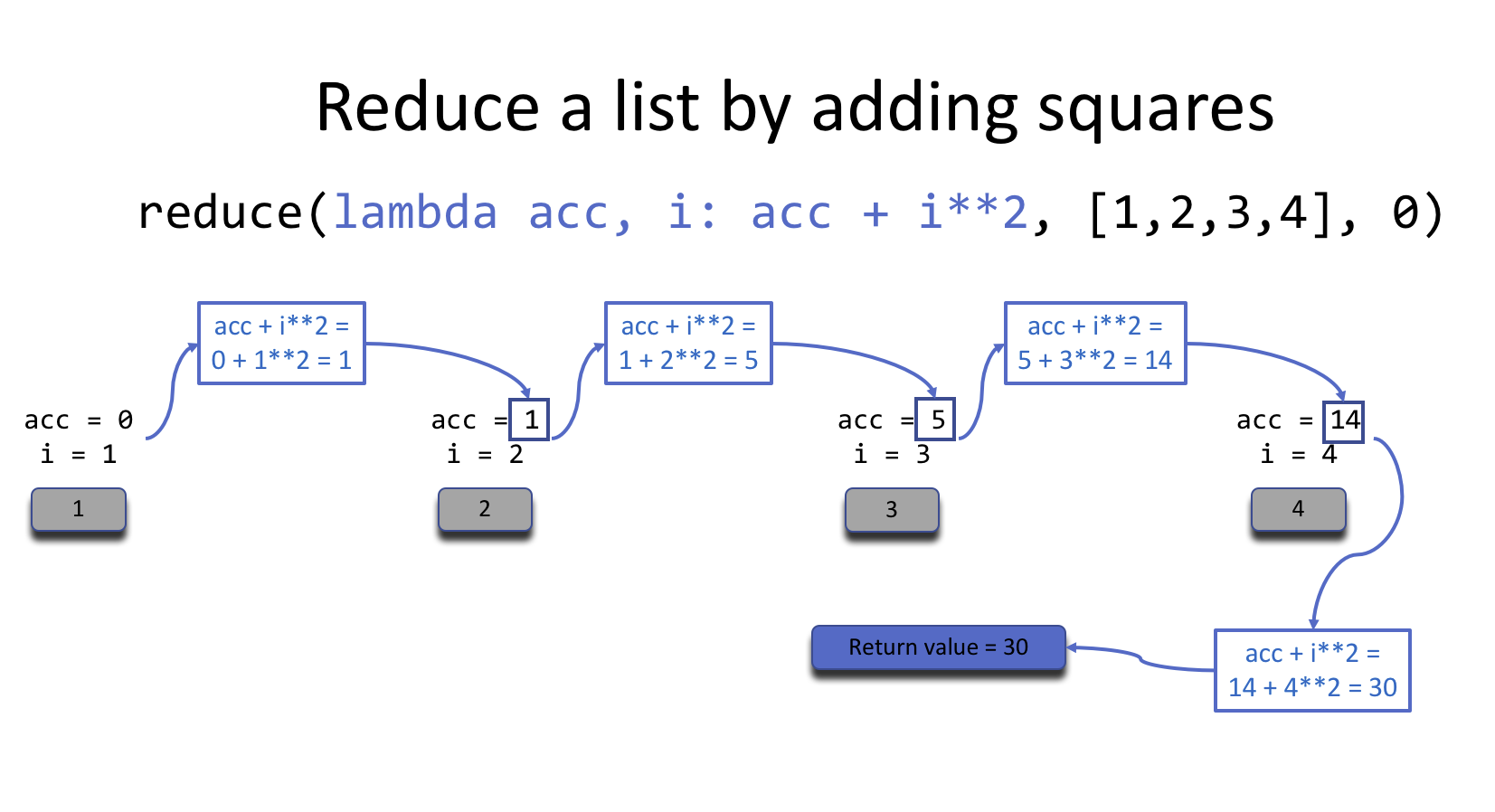
When using reduce with this update function, the square of each item gets added onto the accumulator acc.

map, filter and reduce all take functions as arguments. Consequently, these function are considered higher order functions. We will explore higher-order functions in the next section.

Check your understanding

exceptions-4-13: What will be returned by the following call to reduce?

reduce(lambda a, i: a + i, [1,2,3], 5)

• (A) [2, 3, 4]
• You are thinking of map, not reduce. Reduce takes an initial value and updates this value based on each input.
• (B) 6
• You forgot about the initial value, which in this case was 5. This reduce will start with the accumulator set to 5, then add 1 to the most current subtotal for each value .
• (C) 8
• We are not adding 1, but the value, to the accumulator.
• (D) 11
• This reduce will start with the accumulator set to 5, then add each value to the most current subtotal for each value.

exceptions-4-14: What will be returned by the following call to reduce?

reduce(lambda a, i: a + i, ['1','2','3'])

• (A) '6'
• Adding strings concatenates them! You need to glue the strings together.
• (B) '123'
• When an initial value isn't provided, reduce will use the first value as the initial value. This reduce will start with the accumulator set to '1', then add each string to the right side of most current accumulator.
• (C) 6
• Adding strings concatenates them! You need to glue the strings together.
• (D) '321'
• In this case the item is added to the right of the accumulator, so the strings will accumulate from left to right.

exceptions-4-15: What will be returned by the following call to reduce?

reduce(lambda a, i: i + a, ['1','2','3'])

• (A) '6'
• Adding strings concatenates them! You need to glue the strings together.
• (B) '123'
• In this case the item is added to the left of the accumulator, so the strings will accumulate from right to left .
• (C) 6
• Adding strings concatenates them! You need to glue the strings together.
• (D) '321'
• When an initial value isn't provided, reduce will use the first value as the initial value. This reduce will start with the accumulator set to '1', then add each string to the left side of most current accumulator.

7.3.4. Simultaneous Reductions¶

When computing the average of a sequence, we have been using the following definition of mean.

In [83]: mean = lambda L: sum(L)/len(L)

Unfortunately, this definition does not work with lazy sequences like those created by map and filter.

In [84]: mean(map(int, ['1','2','3']))
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-84-645e397552f2> in <module>()
----> 1 mean(map(int, ['1','2','3']))

<ipython-input-83-696eef189864> in <lambda>(L)
----> 1 mean = lambda L: sum(L)/len(L)

TypeError: object of type 'map' has no len()

The problem is that a lazy sequence has no idea how long it is and in fact it may represent an infinite sequence. A naive attempt to solve this problem might attempt to replace len with the corresponding reduction, but this is still problematic.

In [85]: from functools import reduce

In [86]: from operator import add

In [87]: count = lambda a, i: a + 1

In [88]: mean = lambda L: sum(L)/reduce(count, L, 0)

In [89]: mean(map(int, ['1','2','3']))
---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-89-645e397552f2> in <module>()
----> 1 mean(map(int, ['1','2','3']))

<ipython-input-88-a3b42564febf> in <lambda>(L)
----> 1 mean = lambda L: sum(L)/reduce(count, L, 0)

ZeroDivisionError: division by zero

Again, the issue stems from the fact that the sequence returned by map is lazy, but this time we run into the fact that we can only process this lazy stream once. After the sequence passes through sum it is empty, so the reduce returns 0. Luckily in this case we get an exception, if we hadn’t tried to divide by 0, we may have missed this subtle bug!

The solution to this issue involves computing both the total and count in one pass (i.e. in one reduce). This is accomplished by keeping both accumulators in a tuple and updating both values at each step.

In [90]: from toolz import get

In [91]: sum_count = lambda L: reduce(lambda a, i: (get(0, a) + i, get(1, a) + 1), L, (0, 0))

In [92]: sum_count(map(int, ['1','2','3']))
Out[92]: (6, 3)

We then compose this function with a function that process the tuple of statistics by dividing the total by the count.

In [93]: from toolz import compose, do

In [94]: div_sum_count = lambda tup: get(0, tup)/get(1, tup)

In [95]: mean = compose(div_sum_count,lambda seq: do(print, sum_count(seq)))

In [96]: mean(map(int, ['1', '2', '3']))
(6, 3)
Out[96]: 2.0

We now have a more general definition of mean, one that can process both lists and lazy streams of data.