7.1.1. Fruitful Functions¶

When writing functional programs, we focus on functions that return values, called fruitful functions. In many other languages, a chunk that doesn’t return a value is called a procedure, which we will call non-fruitful. It is worth noting that non-fruitful functions will almost always be side-effecting (what else could they do?). Understanding a program that uses side-effecting functions can be difficult, because the nature of the side-effect is not obvious in the function call. Consequently, functional programs involve writing pure fruitful functions whenever possible. A pure function is a side-effect free fruitful function, making it referentially transparent.

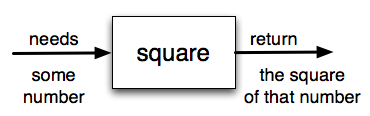
How do we write our own fruitful function? Let’s start by creating a very simple mathematical function that we will call square. The square function will take one number as a parameter and return the result of squaring that number. Here is the black-box diagram with the Python code following.

In [1]: def square(x):
   ...:     """ Return the square of the number x"""
   ...:     y = x * x
   ...:     return y
   ...: 

In [2]: number = 10

In [3]: result = square(number)

In [4]: result
Out[4]: 100

The return statement is followed by an expression which is evaluated. Its result is returned to the caller as the “fruit” of calling this function. Because the return statement can contain any Python expression we could have avoided creating the temporary variable y and simply used return x*x. On the other hand, using temporary variables like y in the program above makes the code easier to read and debug. Temporary variables assigned inside the body of a function are local variables and have a scope that includes the body of the functions.

As with lambda expressions, defining a new function does not make the function run. To do that we need a function call using the same syntax as used with built-in functions and lambda expressions.

Notice something important here. The name of the variable we pass as an argument — number — has nothing to do with the name of the formal parameter — x. It is as if x = toSquare is executed when square is called. It doesn’t matter what the value was named in the caller. In square, its name is x. You can see this very clearly in codelens, where the global variables and the local variables for the square function are in separate boxes.

As you step through the example in codelens notice that the return statement not only causes the function to return a value, but it also returns the flow of control back to the place in the program where the function call was made.

Another important thing to notice as you step through this codelens demonstration is the movement of the red and green arrows. Codelens uses these arrows to show you where it is currently executing. Recall that the red arrow always points to the next line of code that will be executed. The light green arrow points to the line that was just executed in the last step.

When you first start running this codelens demonstration you will notice that there is only a red arrow and it points to line 1. This is because line 1 is the next line to be executed and since it is the first line, there is no previously executed line of code.

When you click on the forward button, notice that the red arrow moves to line 5, skipping lines 2 and 3 of the function (and the light green arrow has now appeared on line 1). Why is this? The answer is that function definition is not the same as function execution. Lines 2 and 3 will not be executed until the function is called on line 6. Line 1 defines the function and the name square is added to the global variables, but that is all the def does at that point. The body of the function will be executed later. Continue to click the forward button to see how the flow of control moves from the call, back up to the body of the function, and then finally back to line 7, after the function has returned its value and the value has been assigned to squareResult.

Finally, there is one more aspect of function return values that should be noted. All Python functions return the value None unless there is an explicit return statement with a value other than None. Consider the following common mistake made by beginning Python programmers. As you step through this example, pay very close attention to the return value in the local variables listing. Then look at what is printed when the function returns.

The problem with this function is that even though it prints the value of the square, that value will not be returned to the place where the call was done. Since line 6 uses the return value as the right hand side of an assignment statement, the evaluation of the function will be None. In this case, squareResult will refer to that value after the assignment statement and therefore the result printed in line 7 is incorrect. Typically, functions will return values that can be printed or processed in some other way by the caller.

7.1.2. Void Functions and Side Effects¶

Occasionally, we will also need to write non-fruitful functions, which are also sometimes referred to as procedures or void functions. The figure below illustrates the black-box diagram of a void function. These values, often called arguments or actual parameters, are passed to the function by the user.

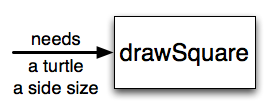
Suppose we’re working with turtles and a common operation we need is to draw squares. It would make sense if we did not have to duplicate all the steps each time we want to make a square. “Draw a square” can be thought of as an abstraction of a number of smaller steps. We will need to provide two pieces of information for the function to do its work: a turtle to do the drawing and a size for the side of the square. We could represent this using the following black-box diagram.

Here is a program containing a function to capture this idea. Give it a try.

Everything that this function does is a side-effect. The import statement adds the turtle library to the main name space (a side-effect). The function definition saves the associated function value to the main namespace (a side-effect). The turtle.Screen call makes an external screen for turtles (a side-effect)... etc. All programs need some part of their code to be side-effecting, if nothing else we need to read data in and output results. The goals in functional programming, regarding side-effect are as follows.

1. Make as many functions as possible pure and fruitful. We will test these functions to confirm that they are correct and once tested, we will know that they are not the source of any bugs in our program.
2. Write small functions and provide a quality name for each. Each function should perform one and only one abstract task.
3. Refactor longer functions by identifying portions of the code that perform some task and putting this code in another function.
4. Always be aware of side-effects and try to capture and contain side-effects in a small number of functions. Side-effecting functions are much hard to test, which is one of the reasons that we will keep them to a minimum.

We will dedicate more time to each of these topics in the upcoming sections.

Check your understanding

exceptions-4-6: What is wrong with the following function definition:

def addEm(x, y, z):
    return x + y + z
    print('the answer is', x + y + z)

• (A) You should never use a print statement in a function definition.
• Although you should not mistake print for return, you may include print statements inside your functions.
• (B) You should not have any statements in a function after the return statement. Once the function gets to the return statement it will immediately stop executing the function.
• This is a very common mistake so be sure to watch out for it when you write your code!
• (C) You must calculate the value of x+y+z before you return it.
• Python will automatically calculate the value x+y+z and then return it in the statement as it is written
• (D) A function cannot return a number.
• Functions can return any legal data, including (but not limited to) numbers, strings, turtles, etc.

exceptions-4-7: What will the following function return?

def addEm(x, y, z):
    print(x + y + z)

• (A) Nothing (no value)
• We have accidentally used print where we mean return. Therefore, the function will return the value None by default. This is a VERY COMMON mistake so watch out! This mistake is also particularly difficult to find because when you run the function the output looks the same. It is not until you try to assign its value to a variable that you can notice a difference.
• (B) The value of x + y + z
• Careful! This is a very common mistake. Here we have printed the value x+y+z but we have not returned it. To return a value we MUST use the return keyword.
• (C) The string 'x + y + z'
• x+y+z calculates a number (assuming x+y+z are numbers) which represents the sum of the values x, y and z.

7.1.3. Program Development¶

At this point, you should be able to look at complete functions and tell what they do. Also, if you have been doing the exercises, you have written some small functions from expressions and list comprehensions. As you write larger functions, you might start to have more difficulty, especially with runtime and semantic errors.

To deal with increasingly complex programs, we are going to suggest a technique called incremental development. The goal of incremental development is to avoid long debugging sessions by adding and testing only a small amount of code at a time.

As an example, suppose you want to find the distance between two points, given by the coordinates \((x_1, y_1)\) and \((x_2, y_2)\). By the Pythagorean theorem, the distance is:

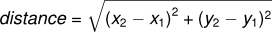
The first step is to consider what a distance function should look like in Python. In other words, what are the inputs (parameters) and what is the output (return value)?

In this case, the two points are the inputs, which we can represent using four parameters. The return value is the distance, which is a floating-point value.

Already we can write an outline of the function that captures our thinking so far.

In [5]: def distance(x1, y1, x2, y2):
   ...:     return 0.0
   ...: 

Obviously, this version of the function doesn’t compute distances; it always returns zero. But it is syntactically correct, and it will run, which means that we can test it before we make it more complicated.

To test the new function, we create a test function. We will use the convention of naming a test function by prepending test_ to the name of the function.

In [6]: def distance(x1, y1, x2, y2):
   ...:     return 0.0
   ...: 

In [7]: def test_distance():
   ...:     assert distance(3,4,0,0) == 5
   ...:     assert distance(3,4,3,4) == 0
   ...: test_distance()
   ...: 
---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-7-833cb8c97e77> in <module>()
      2     assert distance(3,4,0,0) == 5
      3     assert distance(3,4,3,4) == 0
----> 4 test_distance()
      5 

<ipython-input-7-833cb8c97e77> in test_distance()
      1 def test_distance():
----> 2     assert distance(3,4,0,0) == 5
      3     assert distance(3,4,3,4) == 0
      4 test_distance()
      5 

AssertionError: 

Inside the test function, assert statements are used to test the function for various hand computed cases. In this example, we use the Pythagorean triple (\(3^2+4^2=5^2\)) and also assert that the distance from a point and itself is 0. An assert statement will be invisible if the expression evaluates to True but throw and exception if it fails.

In [8]: assert "a" == "a"

In [9]: assert "a" == "A"
---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-9-adfa1494f295> in <module>()
----> 1 assert "a" == "A"

AssertionError: 

For now, we follow the test function definition with a call to the test functions. This way, we can quickly check our test by running the file.

At this point we have confirmed that the function is syntactically correct, and we can start adding lines of code. After each incremental change, we test the function again. If an error occurs at any point, we know where it must be — in the last line we added.

A logical first step in the computation is to find the differences x₂- x₁ and y₂- y₁. We will store those values in temporary variables named dx and dy.

In [10]: def distance(x1, y1, x2, y2):
   ....:     dx = x2 - x1
   ....:     dy = y2 - y1
   ....:     return 0.0
   ....: 

In [11]: def test_distance():
   ....:     assert distance(3,4,0,0) == 5
   ....:     assert distance(3,4,3,4) == 0
   ....: test_distance()
   ....: 
---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-11-833cb8c97e77> in <module>()
      2     assert distance(3,4,0,0) == 5
      3     assert distance(3,4,3,4) == 0
----> 4 test_distance()
      5 

<ipython-input-11-833cb8c97e77> in test_distance()
      1 def test_distance():
----> 2     assert distance(3,4,0,0) == 5
      3     assert distance(3,4,3,4) == 0
      4 test_distance()
      5 

AssertionError: 

Next we compute the sum of squares of dx and dy.

In [12]: def distance(x1, y1, x2, y2):
   ....:     dx = x2 - x1
   ....:     dy = y2 - y1
   ....:     dsquared = dx**2 + dy**2
   ....:     return 0.0
   ....: 

In [13]: def test_distance():
   ....:     assert distance(3,4,0,0) == 5
   ....:     assert distance(3,4,3,4) == 0
   ....: test_distance()
   ....: 
---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-13-833cb8c97e77> in <module>()
      2     assert distance(3,4,0,0) == 5
      3     assert distance(3,4,3,4) == 0
----> 4 test_distance()
      5 

<ipython-input-13-833cb8c97e77> in test_distance()
      1 def test_distance():
----> 2     assert distance(3,4,0,0) == 5
      3     assert distance(3,4,3,4) == 0
      4 test_distance()
      5 

AssertionError: 

Again, we could run the program at this stage and check the value of dsquared (which should be 25).

Finally, using the fractional exponent 0.5 to find the square root, we compute and return the result.

In [14]: def distance(x1, y1, x2, y2):
   ....:     dx = x2 - x1
   ....:     dy = y2 - y1
   ....:     dsquared = dx**2 + dy**2
   ....:     result = dsquared**0.5
   ....:     return result
   ....: 

In [15]: def test_distance():
   ....:     assert distance(3,4,0,0) == 5
   ....:     assert distance(3,4,3,4) == 0
   ....: test_distance()
   ....: 

If that works correctly, you are done. When using assert statements, silence is golden, meaning that when won’t hear anything from our test function when our function passes the tests. No AssertionErrors. Otherwise, you might want to print the value of result before the return statement.

When you start out, you might add only a line or two of code at a time. As you gain more experience, you might find yourself writing and debugging bigger conceptual chunks. As you improve your programming skills you should find yourself managing bigger and bigger chunks: this is very similar to the way we learned to read letters, syllables, words, phrases, sentences, paragraphs, etc., or the way we learn to chunk music — from individual notes to chords, bars, phrases, and so on.

The key aspects of the process are:

1. Start with a working skeleton program and make small incremental changes. At any point, if there is an error, you will know exactly where it is.
2. Use temporary variables to hold intermediate values so that you can easily inspect and check them.
3. Once the program is working, you might want to consolidate multiple statements into compound expressions, but only do this if it does not make the program more difficult to read.

7.2.1. Default Parameters¶

In an earlier chapter, we contended with the problem of creating a general apply_tax function. One solution was to have the tax rate as a parameter.

In [16]: def apply_tax (rate, cost):
   ....:     return round(rate*cost, 2)
   ....: 

In [17]: apply_tax(1.065, 4.99)
Out[17]: 5.31

It was noted that having to input the same tax rate can be annoying, but also violated the DRY principle. Our first solution to this problem was to use a function factory and a closure to create specific implementations of apply_tax.

In [18]: def make_apply_tax(rate):
   ....:     def apply_tax(cost):
   ....:         return round(rate*cost, 2)
   ....:     return apply_tax
   ....: 

In [19]: apply_tax = make_apply_tax(1.065)

In [20]: apply_tax(4.99)
Out[20]: 5.31

The standard “Pythonic” solution to this problem is to use a default parameter for the tax rate. The default value is selected to be some convenient and typical value and the user can either use this default or provide their own.

In [21]: def apply_tax(cost, rate=1.065):
   ....:      return round(rate*cost, 2)
   ....: 

In [22]: apply_tax(4.99)
Out[22]: 5.31

In [23]: apply_tax(4.99, 1.07)
Out[23]: 5.34

In [24]: apply_tax(4.99, rate=1.07)
Out[24]: 5.34

Note that we can give an alternate value for the default value positionally (by adding a second parameter) or by explicitly assigning a value to the parameter (rate=1.07).

Default parameters must follow all regular (positional) parameters.

7.2.2. Variable Arity Functions¶

So far, our functions have had a fixed arity, a fixed number of inputs. If we define the function add to take two inputs, calls to this function will work if and only if it is supplied two arguments.

In [25]: add = lambda x,y: x + y

In [26]: add(1,2)
Out[26]: 3

In [27]: add(1,2,3)
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-27-1315ff1935d2> in <module>()
----> 1 add(1,2,3)

TypeError: <lambda>() takes 2 positional arguments but 3 were given

In [28]: add(1)
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-28-916e497b8c78> in <module>()
----> 1 add(1)

TypeError: <lambda>() missing 1 required positional argument: 'y'

Here is an interesting fact about the print functions, it can take a variable number of inputs.

In [29]: print("A")
A

In [30]: print(1,2,3)
1 2 3

How does that work? It turns out that we can design similar functions using the variable arguments in our definition. When we use *args as a parameter, Python will accept any number of arguments and give them to us in a tuple named args. You should think of *args to represent zero or more arguments stored in a tuple named args. In the case of the add function, we can simply apply the sum function to this tuple to get the sum of all the numbers.

In [31]: add = lambda *args: sum(args) #*

In [32]: add(1)
Out[32]: 1

In [33]: add(1,2,3)
Out[33]: 6

In [34]: add()
Out[34]: 0

While it is traditional to use args for a variable number of arguments, you can use a different name if your like.

In [35]: add = lambda *bobs: sum(bobs) #*

In [36]: add(1)
Out[36]: 1

In [37]: add(1,2,3)
Out[37]: 6

In [38]: add()
Out[38]: 0

We can combine a variable number of arguments with regular parameters, for example, if we wanted to design add to take one or more parameters, you would start with the required one parameter, then add the *args for zero or more additional parameters.

In [39]: add = lambda first, *args: first + sum(args) #*

In [40]: add(1)
Out[40]: 1

In [41]: add(1,2,3)
Out[41]: 6

In [42]: add()
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-42-09e9fb56b0a4> in <module>()
----> 1 add()

TypeError: <lambda>() missing 1 required positional argument: 'first'

7.2.3. Keyword Arguments¶

Just as using *args allows construction of functions with any number of arguments, we can use the **kwargs to provide any number of keyword arguments. Keyword arguments, like default parameters, are used to define values by name as opposed to position.

To define a function that accepts keyword arguments, we add the special **kwargs parameter to the end of the parameter list.

In [43]: def f(**kwargs): #**
   ....:     print('The keywords and values are', kwargs)
   ....: 

When calling such a function, we provide the keyword arguments by unpacking a dictionary of keywords and the corresponding values.

In [44]: f(x = 2, y = 3)
The keywords and values are {'y': 3, 'x': 2}

Notice that all of the keyword arguments are returned in a dictionary named kwargs. The keys of this dictionary are the strings for each keyword and the value are the corresponding argument values.

Let’s return to the apply_tax example. Another solution to the problem is to define the function to allow for keyword arguments, then check these arguments for the 'rate' keyword.

In [45]: from toolz import get

In [46]: def apply_tax(cost, **kwargs): #**
   ....:     if 'rate' in kwargs:
   ....:         rate = get('rate', kwargs)
   ....:     else:
   ....:         rate = 1.065
   ....:     return round(rate*cost, 2)
   ....: 

In [47]: apply_tax(4.99)
Out[47]: 5.31

In [48]: apply_tax(4.99, rate = 1.07)
Out[48]: 5.34

7.2.4. Unpacking arguments and keywords¶

The *args notation also has a utility in a function call. Applying the * operator to a list unpacks it, passing each entry in the sequence as a argument (separated by commas). Thus, we think of *[1,2,3] as 1,2,3 and add(*[1,2,3]) as add(1,2,3).

In [49]: add(*[1,2,3]) #*
Out[49]: 6

As we can see with the add function defined above, combining a variable number of parameters with the unpacking operator allows us to write and use very general functions. Here we have a function that will work on any number of arguments, as well as on unpacked lists. In particular, applying this function to the list allows us to add up a list of undetermined length!

Unpacking dictionaries with the ** operator is similar to unpacking lists with * operator. In this case, we think of **{'x':5, 'y':2} as returning x=5, y=2.

Here is an example of using keyword unpacking with the apply_tax function that accepts keyword arguments.

In [50]: from toolz import get

In [51]: def apply_tax(cost, **kwargs): #**
   ....:     if 'rate' in kwargs:
   ....:         rate = get('rate', kwargs)
   ....:     else:
   ....:         rate = 1.065
   ....:     return round(rate*cost, 2)
   ....: 

In [52]: apply_tax(4.99, **{'rate':1.07})
Out[52]: 5.34