7.5. Other Examples of Higher Order Functions¶
In this section, we will implement some other common higher-order functions
Many of these functions are implemented in the Python libraries toolz and
cytoolz under the sub module titled functoolz. These two modules have
exactly the same functionality, but the cytoolz functions are implemented
within cython, which means that you get better performance. Unfortunately,
you need a C compiler to install cytoolz, but toolz also has decent
performance approximately equal in performance to similar tools from the
standard library.
Note
You can install these packages using pip from the command line, as shown
below,
pip install toolz cytoolz
or you can run this command inside a jupyter console or notebook.
!pip install toolz cytoolz
7.5.1. Composition¶
Consider the following example, which involves cleaning up a string by removing punctuation, whitespace and upper-case characters.
In [1]: from string import punctuation, whitespace
In [2]: s = '''Success is not final,
...: failure is not fatal:
...: it is the courage to continue that counts.'''
...:
In [3]: remove_punc = lambda s: "".join([ch for ch in s if ch not in punctuation])
In [4]: make_lower_case = lambda s: s.lower()
In [5]: fix_whitespace = lambda s: "".join([" " if ch in whitespace else ch for ch in s])
In [6]: s = remove_punc(s)
In [7]: s = make_lower_case(s)
In [8]: s = fix_whitespace(s)
In [9]: s
Out[9]: 'success is not final failure is not fatal it is the courage to continue that counts'
In this imperative example, we are mutating the value stored as s by
applying one function after the other. We could have composed these three calls
into one call, as follows.
In [10]: s = remove_punc(make_lower_case(fix_whitespace(s)))
In [11]: s
Out[11]: 'success is not final failure is not fatal it is the courage to continue that counts'
What if we want to reuse this code? Of course, we could use a function to make this expression reusable.
In [12]: clean_up = lambda s: remove_punc(make_lower_case(fix_whitespace(s)))
In [13]: s = clean_up(s)
In [14]: s
Out[14]: 'success is not final failure is not fatal it is the courage to continue that counts'
Function composition is so common that it will be useful to abstract the process of composing and applying a function.
Before we construct this function, it is useful to look at the imperative
solution to the problem. We can use a for loop to cycle through the functions
and an accumulator to keep track of the latest value of the output. Also note
that we need to apply the right-most function first, so we will used
reversed to iterate through the list back to front. In addition, we add a
variable number of args to remove the need for using a list as an argument.
In [15]: def compose_imperative(*funcs): #*
....: def new_func(item):
....: output = item
....: for func in reversed(funcs):
....: output = func(output)
....: return output
....: return new_func
....:
In [16]: clean_up = compose_imperative(remove_punc, make_lower_case, fix_whitespace)
In [17]: clean_up(s)
Out[17]: 'success is not final failure is not fatal it is the courage to continue that counts'
The fact that we are using the accumulator pattern indicates that this operation is a reduction. Creating this function adheres to the DRY principle, as we won’t need to explicitly compose functions over and over in our code. In fact, we don’t even need to give this new function a name, but can call it anonymously as follows.
In [18]: compose_imperative(remove_punc,
....: make_lower_case,
....: fix_whitespace)(s)
....:
Out[18]: 'success is not final failure is not fatal it is the courage to continue that counts'
Now that we have recognized that this process is a reduction, we refactor the code accordingly. In this case, it is again important to work through the reversed list to preserve the order of operation of functional composition.
In [19]: from functools import reduce
In [20]: def my_compose(*funcs): #*
....: def new_func(item):
....: return reduce(lambda acc, next_func: next_func(acc), reversed(funcs), item)
....: return new_func
....:
In [21]: my_compose(remove_punc,
....: make_lower_case,
....: fix_whitespace)(s)
....:
Out[21]: 'success is not final failure is not fatal it is the courage to continue that counts'
There is no need to implement this function, as the toolz library includes
an implementation called compose.
In [22]: from toolz import compose
In [23]: compose(remove_punc,
....: make_lower_case,
....: fix_whitespace)(s)
....:
Out[23]: 'success is not final failure is not fatal it is the courage to continue that counts'
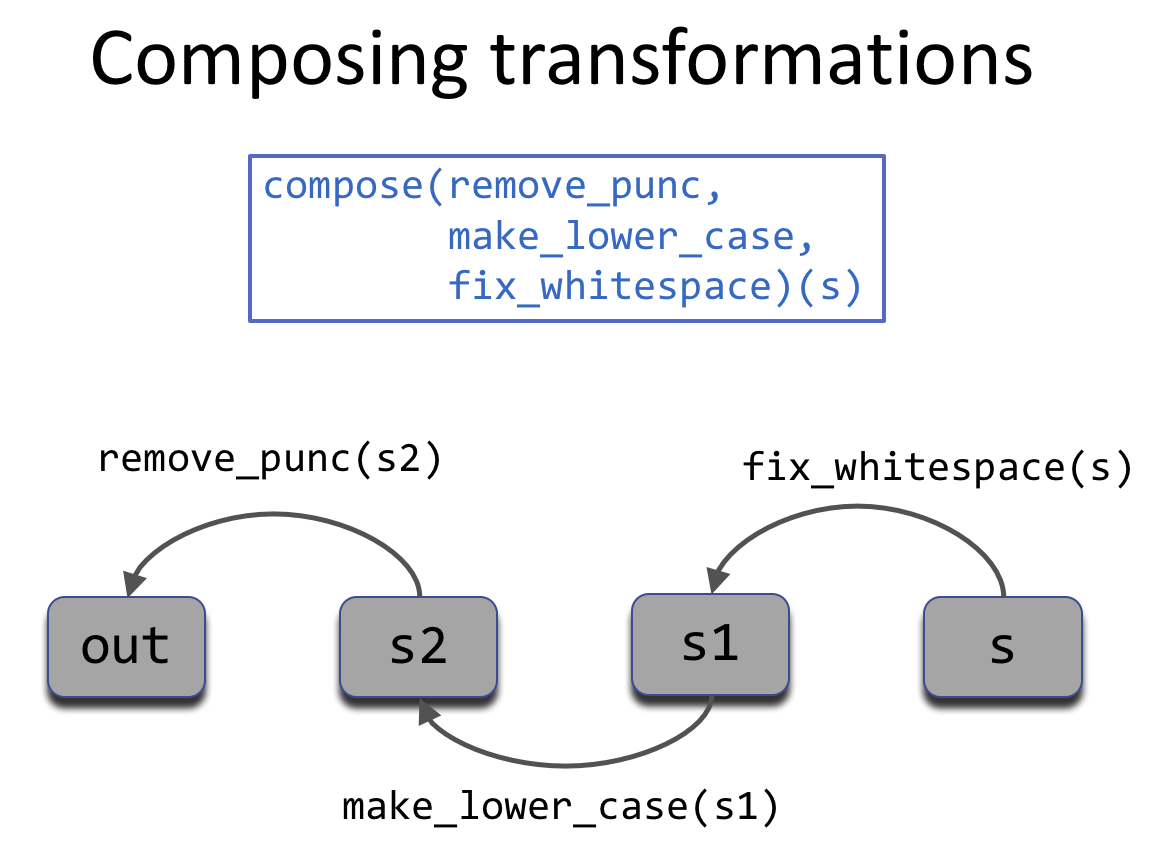
7.5.2. Other types of composition¶
One must always remember that compose passes the input through the functions
from right-to-left. Another composition function included in toolz, pipe,
can be used to push an argument through any number of unary functions from
left-to-right.
In [24]: from toolz import pipe
In [25]: pipe(s , fix_whitespace, make_lower_case, remove_punc)
Out[25]: 'success is not final failure is not fatal it is the courage to continue that counts'
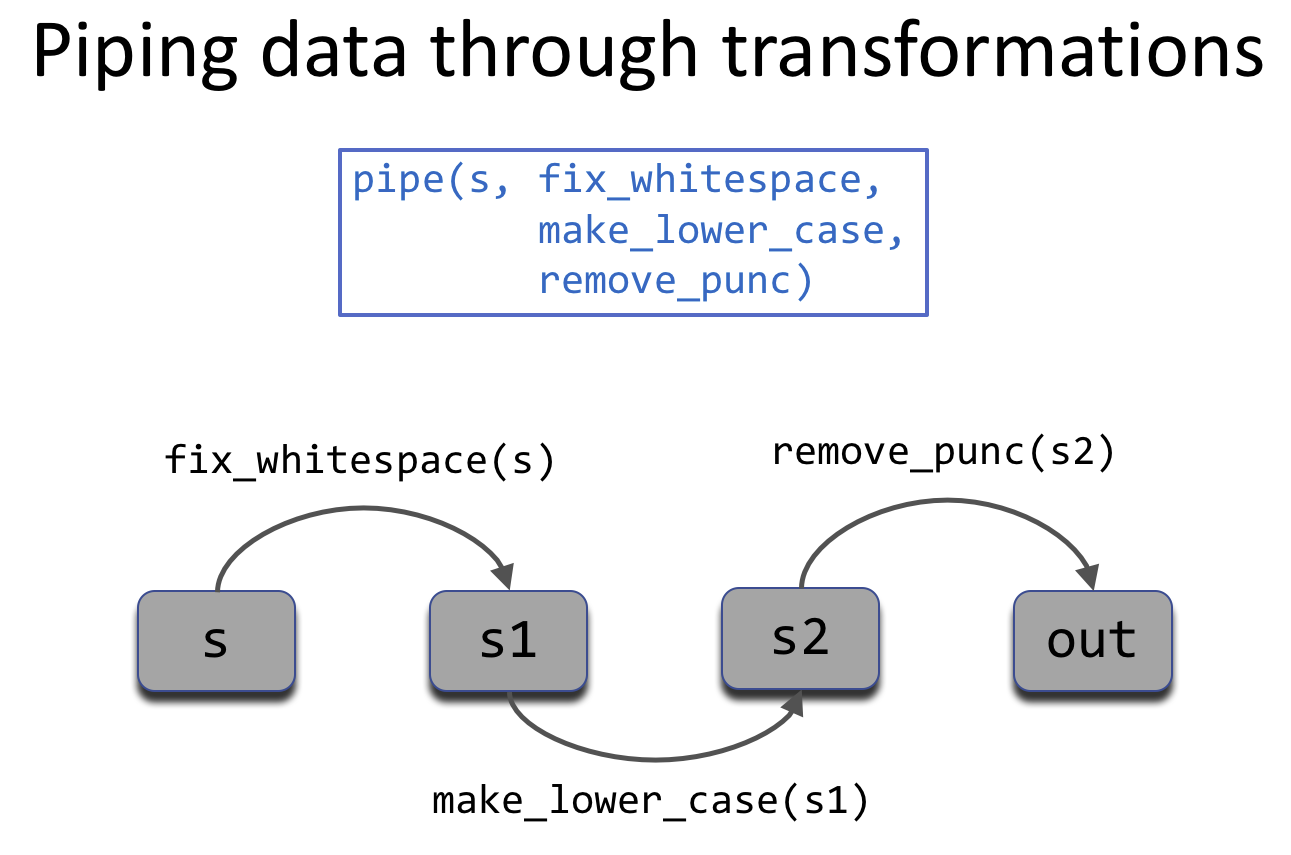
The pipe function is designed for a sequence of unary (one argument)
functions. What if we want to perform a similar, left-to-right sequence of
calls, but with functions with arity greater than 1? Use tread_first! The
first argument of thread_first is the argument val that will be passed
through a sequence of functions. The remaining argument are the functions that
will be allied from left-to-right. thread_first allows a function argument
to be replaced with a tuple in the form of (func, arg1, arg2, ..., argn),
and the subsequent function call will be of the form func(val, arg1, arg2,
..., argn). Note that the first in tread_first indicated that the
argument val will be the first argument in each call.
In [26]: from operator import add, pow, abs, sub
In [27]: from toolz import thread_first
In [28]: thread_first(5, (add, 2), (pow, 2), (sub, 6))
Out[28]: 43
# The above is equivalent to
In [29]: sub(pow(add(5, 2), 2), 6)
������������Out[29]: 43
If, on the other hand, you wish to a pass a value val through a sequence of
functions in the last argument, use thread_last.
In [30]: from toolz import thread_last
In [31]: thread_last(5, (add, 2), (pow, 2), (sub, 6))
Out[31]: -122
# The above is equivalent to
In [32]: sub(6, pow(2, add(2, 5)))
��������������Out[32]: -122
Note
We will show how to use curried functions with pipe in the coming
sections. Also, you will implement your own versions of pipe,
thread_first and thread_last in the exercises found at the end of
the chapter.
7.5.3. Partial Functions¶
In the second chapter, we illustrated how to use a function factory to
generalize the apply_tax function.
In [33]: def make_apply_tax(rate):
....: def apply_tax(cost):
....: return rate*cost
....: return apply_tax
....:
In [34]: rate = 1.065
In [35]: apply_tax = make_apply_tax(rate)
In [36]: apply_tax(1)
Out[36]: 1.065
In [37]: apply_tax(4.55)
���������������Out[37]: 4.84575
A simpler approach to this problem would be to define apply_tax as a two
parameter function, but this would require us to input the tax rate each time
with make a function call (repeated code).
In [38]: def apply_tax(rate, cost):
....: return rate*cost
....: rate = 1.065
....: apply_tax(rate, 1)
....: apply_tax(rate, 4.55)
....:
Out[38]: 4.84575
This apply tax function is definitely easier to understand compared to
make_apply_tax. The traditional method for removing this unneeded
replication of one or more arguments is the use of a partial function. A
partial function is used to call a base function, but fixes the values of
some of the arguments of this base function. We can use partial from the
functools library to create partial functions.
In [39]: from functools import partial
In [40]: my_apply_tax = partial(apply_tax, 1.065)
In [41]: my_apply_tax(1)
Out[41]: 1.065
In [42]: my_apply_tax(4.55)
���������������Out[42]: 4.84575
This solution provides a nice compromise between the complexity of a function
factory and the unneeded replication of a second parameter. First, we don’t
need to use the more complex nested functions; but we can still save the
replication of the rate parameter in each function call.
So what is happening here? Clearly partial is a higher-order function (it
returns another function). One way to think about this: a call to a partial
function calls apply_tax with rate fixed at 1.065, leaving the cost
parameter as the only remaining formal parameter.
partial makes it easy to fill in the left-most formal parameters, but what
if we had ordered the parameters in reverse?
In [43]: def apply_tax_reverse(cost, rate):
....: return rate*cost
....:
Using partial here requires us to wrap our function in a lambda that
reverses the order of the arguments.
In [44]: my_apply_tax = partial(lambda rate, cost: apply_tax_reverse(cost, rate), 1.065)
In [45]: my_apply_tax(1)
Out[45]: 1.065
In [46]: my_apply_tax(4.55)
���������������Out[46]: 4.84575
The toolz library includes a function called flip that can be used to
flip the order of the parameters without needing to create a lambda expression.
In [47]: from toolz import flip
In [48]: my_apply_tax = partial(flip(apply_tax_reverse), 1.065)
In [49]: my_apply_tax(1)
Out[49]: 1.065
In [50]: my_apply_tax(4.55)
���������������Out[50]: 4.84575
Another useful approach is the application of a default parameter. Then we can
use keyword expansion along with partial to create a specialized version of
our function with a different default value. Again, partial saves us from
having to type the alternative value of the keyword more than once.
In [51]: def apply_tax_default(cost, rate=1.05):
....: return rate*cost
....:
In [52]: my_apply_tax = partial(apply_tax_default, ** {"rate":1.065})
In [53]: my_apply_tax(1)
Out[53]: 1.065
In [54]: my_apply_tax(4.55)
���������������Out[54]: 4.84575
Note
Unfortunately some of the built-in python functions like reduce do
not treat optional parameters as keyword arguments and another approach will
need to be used for these functions.
7.5.4. Decorator Functions¶
partial is an example of a decorator function, which is a function that
creates a wrapper around another function. The outer function calls the
original function and then changes or decorates the input and/or output.
For example, when processing text, it is often useful to switch all the text to lower case. We will create a decorator function that can be used to wrap any function that returns a string and ensure that the output is lower case.
In [55]: def lower_out(func):
....: def decorated_func(s):
....: return func(s).lower()
....: return decorated_func
....:
In [56]: def emph(s):
....: return "**{0}**".format(s)
....:
In [57]: decorated_emph = lower_out(emph)
In [58]: decorated_emph("HI")
Out[58]: '**hi**'
This example should make it clear that the decorator function is a higher-order
function, as it returns another function. Decorator functions are a core
feature of Python and there is a special @ notation that makes it easy to
apply a decorator function to the definition of another function.
In [1]: @lower_output
...: def emph(s):
...: return "**{0}**".format(s)
...:
In [2]: emph("HI")
Out[2]: '**hi**'
Using the @ notation on the line(s) above a function definition immediately
decorates the function emph as part of the function definition, removing the
need to use different name for the decorated function.
7.5.5. Currying¶
Currying is another popular functional approach to partial application of functions. Recall that the arity of a function is the number of arguments the function takes. We can implement functions with arity higher than 1 using a single-arith functions with technique called currying, which is illustrated below.
In [59]: curried_pow = lambda x: lambda y: x**y
In [60]: curried_pow(2)(3)
Out[60]: 8
In Python, this approach results in replacing the commas between arguments with multiple function calls, one after the other.
Note
Functional languages like Haskell and Scala have implemented currying as a basic design feature and using this approach in these language is considered syntactically cleaner.
The advantage to curried functions is we get partial application for free.
In [61]: exp2 = curried_pow(2)
In [62]: exp2(1)
Out[62]: 2
In [63]: exp2(3)
�����������Out[63]: 8
A better approach to currying in Python is the use of a decorator. The
toolz and cytoolz libraries provide a decorator function called
curry that can be used to convert any function definition into a curried
function.
In [1]: from toolz import curry
In [2]: @curry
...: def pow(x,y):
...: return x**y
...:
In [3]: # Partial application is possible
In [4]: exp2 = pow(2)
In [5]: exp2(3)
Out[5]: 8
In [6]: # But we can also call the function with full arity
In [7]: pow(3,3)
Out[7]: 27
In [8]: # this works for any number of arguments
In [9]: @curry
...: def f(x,y,z):
...: return z*(x + y)
...:
In [10]: g = f(2)
In [11]: g(3,4)
Out[11]: 20
In [12]: h = f(2,3)
In [13]: h(4)
Out[13]: 20
Let’s implement a simple version of this currying decorator. We will use the
signature function from the inspect module to determine the arity of a
function and return a partial function when provided with less then the full
number of arguments.
In [1]: from inspect import signature
In [2]: from functools import partial
In [3]: def my_curry(func):
...: arity = len(signature(func).parameters)
...: def dec_func(*myargs):
...: if len(myargs) < arity:
...: return partial(func, *myargs)
...: else:
...: return func(*myargs)
...: return dec_func
...:
In [4]: @my_curry
...: def f(x,y,z):
...: return z*(x + y)
...:
In [5]: g = f(2)
In [6]: g(3,4)
Out[6]: 20
In [7]: h = f(2,3)
In [8]: h(4)
Out[8]: 20
In [9]: f(2,3,4)
Out[9]: 20
Note
As stated, this is a simple version of the function which ignores key Python
features like variable and keyword unpacking, as well as default parameters.
Be sure to use curry decorator from the toolz in practice.
What if you wanted to to supply the first and third argument for an arity 3
curried function? In this case, we can make use of the flip function from
toolz. This function calls a function with the arguments flipped.
In [64]: from toolz.functoolz import flip
In [65]: from math import pow
In [66]: flip(pow, 2, 3)
Out[66]: 9.0
In [67]: pow(2,3)
�������������Out[67]: 8.0
flip works well with a curried function, as a flip will give access to the
third parameter while leaving the second parameter empty and returning a partial
function.
In [1]: from toolz import curry
In [2]: from toolz.functoolz import flip
In [3]: @curry
...: def f(x,y,z):
...: return 1*x + 10*y + 100*z
...:
In [4]: h = flip(f(1), 2)
# Note that is is the middle number/parameter that is changing
In [5]: h(3)
Out[5]: 231
In [6]: h(2)
Out[6]: 221
In [7]: h(1)
Out[7]: 211
Note
You will implement your own version of flip in the exercises.
7.5.6. Other useful curried functions from toolz¶
Many of the functions from the toolz library have been designed with
currying in mind. Furthermore, curried versions of most functions can be
imported from toolz.curried.
One example of such a function is get, which can be used to get one more more
entries from a row of a table.
In [68]: from toolz.curried import get
In [69]: table = [[1, 2, 3],
....: [4, 5, 6],
....: [7, 8, 9],
....: [10, 11,12],
....: [13, 14,15]]
....:
In [70]: get(2, table[0])
Out[70]: 3
In [71]: col1 = [get(2, row) for row in table]
In [72]: col1
Out[72]: [3, 6, 9, 12, 15]
get also takes a list in the first position and in this case returns all of
the selected columns of the table.
In [73]: mixed_up = [get([2, 0, 1], row) for row in table]
In [74]: mixed_up
Out[74]: [(3, 1, 2), (6, 4, 5), (9, 7, 8), (12, 10, 11), (15, 13, 14)]
Using the curried version of this function makes it easy to combine it with
map. The final result is the ability to quickly access selected columns
from a table.
In [75]: list(map(get(2), table))
Out[75]: [3, 6, 9, 12, 15]
In the first line, we are passing the partial function get(2), which will
select the third item when applied to a row. Then map is used to apply
get(2) to each row in the matrix. Similarly, we can make a partial
application or get by passing in a list of indices.
In [76]: list(map(get([2,0,1]), table))
Out[76]: [(3, 1, 2), (6, 4, 5), (9, 7, 8), (12, 10, 11), (15, 13, 14)]
This pattern has been abstracted in the toolz library in the form of
pluck, where pluck(2, table) is functionally equivalent to map(get(2),
table). Similar to combining map with get, pluck is a lazy
construct that needs to be forced to completion.
In [77]: from toolz.curried import pluck
In [78]: list(pluck([2,0,1], table))
Out[78]: [(3, 1, 2), (6, 4, 5), (9, 7, 8), (12, 10, 11), (15, 13, 14)]
The curried version of pluck can be used to create useful partial functions.
In [79]: mixup_table = pluck([2,0,1])
In [80]: output = mixup_table(table)
In [81]: list(output)
Out[81]: [(3, 1, 2), (6, 4, 5), (9, 7, 8), (12, 10, 11), (15, 13, 14)]
Keep in mind that using pipe to combine actions on a list or table provides
a readable description of a sequence of transformations. In particular, an
application of pipe reads in the natural direction, left-to-right. Suppose
that we have a table of hours worked for all employees over a period of weeks
and we wish to quickly compute the number of hours worked by a particular
employee, Ann.
In [82]: hours = [["Name", "Week", "Hours Worked"],
....: ["Ann", 1, 40],
....: ["Bob", 1, 55],
....: ["Alice", 1, 22],
....: ["Ann", 2, 45],
....: ["Bob", 2, 30],
....: ["Alice", 2, 32],
....: ["Ann", 3, 30],
....: ["Bob", 3, 50],
....: ["Alice", 3, 42]]
....:
This process can be accomplished in the following way.
- Pluck the columns of interest from the table, namely hours worked and name.
- Filter the new table using the name column.
- Reduce this filtered list to the total hours worked by
Ann.
Separately, this can be accomplished as follows.
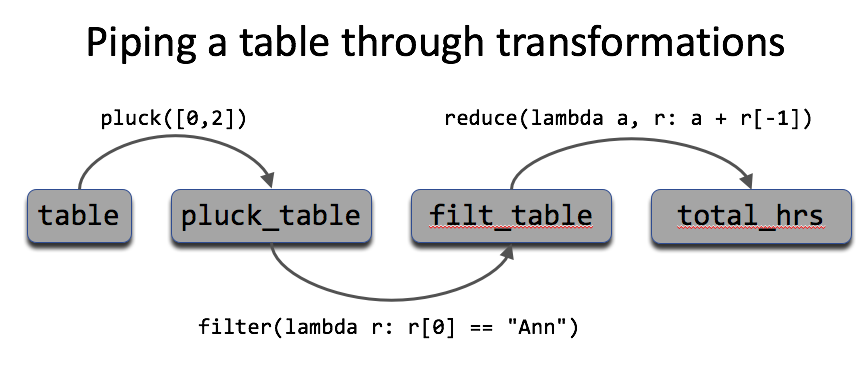
In [83]: pluck_table = pluck([0, 2], hours)
In [84]: filt_table = filter(lambda r: r[0] == "Ann", pluck_table)
In [85]: tot_hour = reduce(lambda a, r: a + r[-1], filt_table, 0)
In [86]: tot_hour
Out[86]: 115
Careful inspection of this solution shows the table piping through a series of transformations, as illustrated in the following figure.
We can clean up much of the unnecessary complexity created by the temporary
variables using the pipe function along with curried versions of pluck,
filter and reduce.
In [87]: from toolz import pipe
In [88]: from toolz.curried import filter, pluck
In [89]: from functools import reduce, partial
# We create a lambda around reduce to input the initial value
In [90]: tot_hours = pipe(hours,
....: pluck([0,2]),
....: filter(lambda r: r[0] == "Ann"),
....: lambda table: reduce(lambda a, r: a + r[-1], table, 0))
....:
In [91]: tot_hours
Out[91]: 115
Note
Due to the fact that reduce does not treat the optional parameter
initial as a keyword argument, we couldn’t use partial or currying to
set this value, and were forced to wrap the function in a lambda expression to
achieve this result.
Note
This is useful when transitioning from writing imperative programs to writing functional programs. Anytime that you want to write code like this:
x = f(x)
x = g(x)
x = h(x)
transform this pattern using pipe and curried or partial functions, as
follows.
pipe(x,
f,
g,
h)
Another mind-bending use of the curried functions from toolz is the curried
version of curry. In addition to being used to create curried functions
as when applied as a decorator, the curried curry can be applied to other
functions. The end result is the ability to create a curried version of a
previously defined function, even the built-in Python functions.
We will illustrate by continuing the example using map and get(2).
By constructing a curried map, we can now easily define a partial function
that will make a new table that contains only column 3.
In [92]: from toolz.curried import curry
In [93]: map = curry(map)
In [94]: get_col_3 = map(get(2))
In [95]: list(get_col_3(table))
Out[95]: [3, 6, 9, 12, 15]
7.5.7. A functional approach to table joins¶
In an earlier section, we illustrated how to use list comprehensions for various
table joining operations (inner-join, left-outer-join, etc.) We can use the
higher-order function from the toolz library to abstract these patterns, but
first we need to refactor the original solution using helper functions.
Consider the original solution given below.
In [96]: hours = [["Alice", 43],
....: ["Bob", 37],
....: ["Fred", 15]]
....:
In [97]: titles = [["Alice", "Manager"],
....: ["Betty", "Consultant"],
....: ["Bob", "Assistant"]]
....:
In [98]: raw_inner_join = [(left_row, right_row)
....: for left_row in hours
....: for right_row in titles
....: if left_row[0] == right_row[0]]
....:
In [99]: raw_inner_join
Out[99]: [(['Alice', 43], ['Alice', 'Manager']), (['Bob', 37], ['Bob', 'Assistant'])]
To compare the rows, we needed to unpack the right key elements. Let’s refactor
these operation into key functions that are used to compare the two rows (left
and right key functions). In this example, the rows are matched based on the name (get(0) for both).
In [100]: left_key = get(0)
In [101]: right_key = get(0)
In [102]: inner_join = [(lrow, rrow)
.....: for lrow in hours for rrow in titles
.....: if left_key(lrow) == right_key(rrow)]
.....:
In [103]: inner_join
Out[103]: [(['Alice', 43], ['Alice', 'Manager']), (['Bob', 37], ['Bob', 'Assistant'])]
The toolz function join abstracts this pattern and can be used to hide
the details of a join. The function join takes the left key function, left
sequence, right key function, and right sequence; in that order. It returns a
table of rows joined in a tuple.
In [104]: from toolz import join
In [105]: left_key = get(0)
In [106]: right_key = get(0)
In [107]: inner_join = join(left_key, hours, right_key, titles)
In [108]: inner_join
Out[108]: <generator object join at 0x10fd48888>
Notice that join returns a lazy sequence. This can be useful for joining tables when one of the tables is very large. More details will be given in a later section.
In [109]: list(inner_join)
Out[109]: [(['Alice', 43], ['Alice', 'Manager']), (['Bob', 37], ['Bob', 'Assistant'])]
Note
The join function returns a tuple of rows. Frequently we would follow up
with a map that cleans up each row into the desired form.
join can also be used for outer joins by changing the default value of the
parameters left_default and/or right_default to None.
Consider a left-out-join. In this case we always want to keep the left row,
even when there is no corresponding right-hand row. Those we replace the missing
right-hand row with None by default by setting right_default=None
In [110]: left_outer_join = join(left_key, hours,
.....: right_key, titles,
.....: right_default=None)
.....:
In [111]: list(left_outer_join)
Out[111]:
[(['Alice', 43], ['Alice', 'Manager']),
(['Bob', 37], ['Bob', 'Assistant']),
(['Fred', 15], None)]
Notice that we use right_default=None to get a left outer join.
Similarly, we achieve a right-outer-join by setting left_default=None.
In [112]: right_outer_join = join(left_key, hours,
.....: right_key, titles,
.....: left_default=None)
.....:
In [113]: list(right_outer_join)
Out[113]:
[(['Alice', 43], ['Alice', 'Manager']),
(None, ['Betty', 'Consultant']),
(['Bob', 37], ['Bob', 'Assistant'])]
A full outer join is constructed by setting both defaults to None.
In [114]: outer_join = join(left_key, hours,
.....: right_key, titles,
.....: left_default=None,
.....: right_default=None)
.....:
In [115]: list(outer_join)
Out[115]:
[(['Alice', 43], ['Alice', 'Manager']),
(None, ['Betty', 'Consultant']),
(['Bob', 37], ['Bob', 'Assistant']),
(['Fred', 15], None)]
7.5.8. Memiozation (Optional)¶
Second, we need sequence helper functions that determine which values should be kept from the respective rows (left and right sequence functions).
One of the problems with recursive functions, especially if they are not tail-recursive or have not been refactored to use an accumulator, is the number of replicated function calls that get made. To see this, we create a decorator function that will use a global dictionary to track the number of calls for each unique argument. We then apply this decorator function to a recursive function that generates the nth fibonacci number.
In [116]: call_dict = {}
In [117]: def fib_with_call_dict(n):
.....: call_dict[n] = call_dict.get(n, 0) + 1
.....: return n if n < 2 else fib_with_call_dict(n-1) + fib_with_call_dict(n-2)
.....:
In [118]: fib_with_call_dict(12)
Out[118]: 144
In [119]: call_dict
��������������Out[119]:
{0: 89,
1: 144,
2: 89,
3: 55,
4: 34,
5: 21,
6: 13,
7: 8,
8: 5,
9: 3,
10: 2,
11: 1,
12: 1}
In [120]: total_calls_to_fib = sum( val for val in call_dict.values())
In [121]: total_calls_to_fib
Out[121]: 465
We see that, even for a small value of n, we get a larger number of calls
for each of the numbers less than n. One solution to this problem is
memiozation, which involves decorating our function and using a dictionary
to remember the output of previous calls. First, we will implement a closure
that includes a reference to a dictionary. Whenever we know the return value
for a specific argument, we will save it in our dictionary. Furthermore, we
will query the dictionary each time our function is called, and we will
immediately return the solution if saved in the dictionary.
In [122]: def make_fib_with_dict():
.....: return_dict = {}
.....: def fib_with_dict(n):
.....: if n in return_dict:
.....: return return_dict[n]
.....: else:
.....: return_dict[n] = output = n if n < 2 else fib_with_call_dict(n-1) + fib_with_call_dict(n-2)
.....: return output
.....: return fib_with_dict
.....:
In [123]: fib_with_dict = make_fib_with_dict()
In [124]: fib_with_dict(12)
Out[124]: 144
Let’s add some tooling to this function to track the number of calls that are immediately satisfied by the dictionary return.
In [125]: dict_calls = 0
In [126]: recursive_calls = 0
In [127]: def make_fib_with_dict():
.....: return_dict = {}
.....: def fib_with_dict(n, dict_calls, rec_calls):
.....: if n in return_dict:
.....: return return_dict[n], dict_calls + 1, rec_calls
.....: else:
.....: output, dict_calls, rec_calls = (n, 0, 1) if n < 2 else [sum(a, b) for a, b in zip(fib_with_call_dict(n-1, dict_calls, rec_calls), fib_with_call_dict(n-2, dict_calls, rec_calls))]
.....: return output, dict_calls, rec_calls + 1
.....: return fib_with_dict
.....:
In [128]: fib_with_dict = make_fib_with_dict()
In [129]: fib_with_dict(12, 0, 0)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-129-d8e40bb07861> in <module>()
----> 1 fib_with_dict(12, 0, 0)
<ipython-input-127-73d87a41c928> in fib_with_dict(n, dict_calls, rec_calls)
5 return return_dict[n], dict_calls + 1, rec_calls
6 else:
----> 7 output, dict_calls, rec_calls = (n, 0, 1) if n < 2 else [sum(a, b) for a, b in zip(fib_with_call_dict(n-1, dict_calls, rec_calls), fib_with_call_dict(n-2, dict_calls, rec_calls))]
8 return output, dict_calls, rec_calls + 1
9 return fib_with_dict
TypeError: fib_with_call_dict() takes 1 positional argument but 3 were given
The toolz/cytoolz modules provide a memoize function that can be applied
to a function or used as a dictionary.
In [130]: from toolz.functoolz import memoize
# You definite don't want to call this without memoize
In [131]: def fib_print(n):
.....: print("Computing fib({0})".format(n))
.....: return n if n < 2 else fib_print(n-1) + fib_print(n-2)
.....:
In [132]: mem_fib = memoize(fib_print)
In [133]: mem_fib(12)
Computing fib(12)
Computing fib(11)
Computing fib(10)
Computing fib(9)
Computing fib(8)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(8)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(9)
Computing fib(8)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(10)
Computing fib(9)
Computing fib(8)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(8)
Computing fib(7)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(6)
Computing fib(5)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(4)
Computing fib(3)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Computing fib(1)
Computing fib(2)
Computing fib(1)
Computing fib(0)
Out[133]: 144
Note that memoize also works as a decorator.
@memoize
def fib(n)
return n if n < 2 else fib(n-1) + fib(n-2)
We can then check this dictionary and
immediately return a value that was previously calculated. Since we need to
mutate the dictionary, it will be defined as an external local variable and
declared using the nonlocal statement in the inner function.
In [134]: def memioze(func):
.....: return_values = {}
.....: def dec_func(n):
.....: nonlocal return_values
.....: if n in return_values:
.....: return return_values[n]
.....: else:
.....: output = func(n)
.....: return_values[n] = output
.....: return output
.....: return_values[n]
.....: return dec_func
.....:
In [135]: def fib(n):
.....: return n if n < 2 else fib(n-1) + fib(n-2)
.....:
In [136]: call_dict = {}
In [137]: fib(12)
Out[137]: 144
In [138]: call_dict
��������������Out[138]: {}