2.1. Transforming Simple Data with Expressions¶
2.1.1. Statements and Expressions¶
A statement is an instruction that the Python interpreter can execute. We
have only seen the assignment statement so far. Some other kinds of statements
that we’ll see shortly are while statements, for statements, if
statements, and import statements. (There are other kinds too!)
An expression is a combination of values, variables, operators, and calls to
functions. Expressions need to be evaluated. If you ask Python to print an
expression, the interpreter evaluates the expression and displays the
result.
In [1]: print(1 + 1)
In [1]: print(len("hello"))
In this example len is a built-in Python function that returns the number
of characters in a string. We’ve previously seen the print and the
type functions, so this is our third example of a function!
The evaluation of an expression produces a value, which is why expressions can appear on the right hand side of assignment statements. A value all by itself is a simple expression, and so is a variable. Evaluating a variable gives the value that the variable refers to.
In [1]: y = 3.14
In [1]: x = len("hello")
In [1]: x
In [1]: y
Note that when we enter the assignment statement, y = 3.14, only the prompt
is returned. There is no value. This is due to the fact that statements, such
as the assignment statement, do not return a value. They are simply executed.
On the other hand, the result of executing the assignment statement is the
creation of a reference from a variable, y, to a value, 3.14. When we
execute the print function working on y, we see the value that y is
referring to. In fact, evaluating y by itself results in the same response.
2.1.2. Operators and Operands¶
Operators are special tokens that represent computations like addition, multiplication and division. The values the operator works on are called operands.
The following are all legal Python expressions whose meaning is more or less clear:
20 + 32
hour - 1
hour * 60 + minute
minute / 60
5 ** 2
(5 + 9) * (15 - 7)
The tokens +, -, and *, and the use of parenthesis for grouping,
mean in Python what they mean in mathematics. The asterisk (*) is the
token for multiplication, and ** is the token for exponentiation.
Addition, subtraction, multiplication, and exponentiation all do what you
expect.
In [1]: 2 + 3
In [1]: 2 - 3
In [1]: 2 * 3
In [1]: 2 ** 3
In [1]: 3 ** 2
When a variable name appears in the place of an operand, it is replaced with
the value that it refers to before the operation is performed.
For example, what if we wanted to convert 645 minutes into hours.
In Python 3, division is denoted by the operator token / which always evaluates to a floating point
result.
In [1]: minutes = 645
In [1]: hours = minutes / 60
In [1]: hours
What if, on the other hand, we had wanted to know how many whole hours there
are and how many minutes remain. To help answer this question, Python gives us a second flavor of
the division operator. This version, called integer division, uses the token
//. It always truncates its result down to the next smallest integer (to
the left on the number line).
In [1]: 7 / 4
In [1]: 7 // 4
In [1]: minutes = 645
In [1]: hours = minutes // 60
In [1]: hours
Pay particular attention to the first two examples above. Notice that the
result of floating point division is 1.75 but the result of the integer
division is simply 1. Take care that you choose the correct flavor of the
division operator. If you’re working with expressions where you need floating
point values, use the division operator /. If you want an integer result,
use //.
The modulus operator, sometimes also called the remainder operator or
integer remainder operator works on integers (and integer expressions) and
yields the remainder when the first operand is divided by the second. In Python,
the modulus operator is a percent sign (%). The syntax is the same as for
other operators.
In [1]: quotient = 7 // 3 # This is the integer division operator
In [1]: quotient
In [1]: remainder = 7 % 3
In [1]: remainder
In the above example, 7 divided by 3 is 2 when we use integer division and there is a remainder of 1.
The modulus operator turns out to be surprisingly useful. For example, you can
check whether one number is divisible by another—if x % y is zero, then
x is divisible by y. Also, you can extract the right-most digit or
digits from a number. For example, x % 10 yields the right-most digit of
x (in base 10). Similarly x % 100 yields the last two digits.
Finally, returning to our time example, the remainder operator is extremely useful for doing conversions, say from seconds, to hours, minutes and seconds. If we start with a number of seconds, say 7684, the following program uses integer division and remainder to convert to an easier form. Step through it to be sure you understand how the division and remainder operators are being used to compute the correct values.
(ch02_19_codelens)
Check your understanding
- (A) 4.5
- The / operator does exact division and returns a floating point result.
- (B) 5
- The / operator does exact division and returns a floating point result.
- (C) 4
- The / operator does exact division and returns a floating point result.
- (D) 2
- The / operator does exact division and returns a floating point result.
data-2-26: What value is printed when the following statement executes?
print(18 / 4)
- (A) 4.25
- - The // operator does integer division and returns an integer result
- (B) 5
- - The // operator does integer division and returns an integer result, but it truncates the result of the division. It does not round.
- (C) 4
- - The // operator does integer division and returns the truncated integer result.
- (D) 2
- - The // operator does integer division and returns the result of the division on an integer (not the remainder).
data-2-27: What value is printed when the following statement executes?
print(18 // 4)
- (A) 4.25
- The % operator returns the remainder after division.
- (B) 5
- The % operator returns the remainder after division.
- (C) 4
- The % operator returns the remainder after division.
- (D) 2
- The % operator returns the remainder after division.
data-2-28: What value is printed when the following statement executes?
print(18 % 4)
2.1.3. Order of Operations¶
When more than one operator appears in an expression, the order of evaluation depends on the rules of precedence. Python follows the same precedence rules for its mathematical operators that mathematics does.
- Parentheses have the highest precedence and can be used to force an
expression to evaluate in the order you want. Since expressions in
parentheses are evaluated first,
2 * (3-1)is 4, and(1+1)**(5-2)is 8. You can also use parentheses to make an expression easier to read, as in(minute * 100) / 60, even though it doesn’t change the result. - Exponentiation has the next highest precedence, so
2**1+1is 3 and not 4, and3*1**3is 3 and not 27. Can you explain why? - Multiplication and both division operators have the same
precedence, which is higher than addition and subtraction, which
also have the same precedence. So
2*3-1yields 5 rather than 4, and5-2*2is 1, not 6. - Operators with the same precedence are
evaluated from left-to-right. In algebra we say they are left-associative.
So in the expression
6-3+2, the subtraction happens first, yielding 3. We then add 2 to get the result 5. If the operations had been evaluated from right to left, the result would have been6-(3+2), which is 1.
Note
Due to some historical quirk, an exception to the left-to-right left-associative rule is the exponentiation operator **. A useful hint is to always use parentheses to force exactly the order you want when exponentiation is involved:
In [1]: 2 ** 3 ** 2 # the right-most ** operator gets done first!
In [1]: (2 ** 3) ** 2 # use parentheses to force the order you want!
Check your understanding
- (A) 14
- Using parentheses, the expression is evaluated as (2*5) first, then (10 // 3), then (16-3), and then (13+1).
- (B) 24
- Remember that * has precedence over -.
- (C) 3
- Remember that // has precedence over -.
- (D) 13.667
- Remember that // does integer division.
data-2-29: What is the value of the following expression:
16 - 2 * 5 // 3 + 1
- (A) 768
- Exponentiation has precedence over multiplication, but its precedence goes from right to left! So 2 ** 3 is 8, 2 ** 8 is 256 and 256 * 3 is 768.
- (B) 128
- Exponentiation (**) is processed right to left, so take 2 ** 3 first.
- (C) 12
- There are two exponentiations.
- (D) 256
- Remember to multiply by 3.
data-2-30: What is the value of the following expression:
2 ** 2 ** 3 * 3
2.1.4. Boolean Values and Boolean Expressions¶
The Python type for storing true and false values is called bool, named
after the British mathematician, George Boole. George Boole created Boolean
Algebra, which is the basis of all modern computer arithmetic.
There are only two boolean values. They are True and False. Capitalization
is important, since true and false are not boolean values (remember Python is case
sensitive).
In [1]: True
In [1]: type(True)
In [1]: type(False)
Note
Boolean values are not strings!
It is extremely important to realize that True and False are not strings. They are not
surrounded by quotes. They are the only two values in the data type bool. Take a close look at the
types shown below.
In [1]: type(True)
In [1]: type("True")
A boolean expression is an expression that evaluates to a boolean value.
The equality operator, ==, compares two values and produces a boolean value related to whether the
two values are equal to one another.
In [1]: 5 == 5
In [1]: 5 == 6
In the first statement, the two operands are equal, so the expression evaluates
to True. In the second statement, 5 is not equal to 6, so we get False.
The == operator is one of six common comparison operators; the others are:
x != y # x is not equal to y
x > y # x is greater than y
x < y # x is less than y
x >= y # x is greater than or equal to y
x <= y # x is less than or equal to y
Although these operations are probably familiar to you, the Python symbols are
different from the mathematical symbols. A common error is to use a single
equal sign (=) instead of a double equal sign (==). Remember that =
is an assignment operator and == is a comparison operator. Also, there is
no such thing as =< or =>.
Note too that an equality test is symmetric, but assignment is not. For example,
if a == 7 then 7 == a. But in Python, the statement a = 7
is legal and 7 = a is not. (Can you explain why?)
Check your understanding
-
data-2-31: Which of the following is a Boolean expression? Select all that apply.
- (A) True
- True and False are both Boolean literals.
- (B) 3 == 4
- The comparison between two numbers via == results in either True or False (in this case False), both Boolean values.
- (C) 3 + 4
- 3 + 4 evaluates to 7, which is a number, not a Boolean value.
- (D) 3 + 4 == 7
- 3 + 4 evaluates to 7. 7 == 7 then evaluates to True, which is a Boolean value.
- (E) "False"
- With the double quotes surrounding it, False is interpreted as a string, not a Boolean value. If the quotes had not been included, False alone is in fact a Boolean value.
2.1.5. Logical operators¶
There are three logical operators: and, or, and not. The
semantics (meaning) of these operators is similar to their meaning in English.
For example, x > 0 and x < 10 is true only if x is greater than 0 and
at the same time, x is less than 10. How would you describe this in words? You would say that
x is between 0 and 10, not including the endpoints.
n % 2 == 0 or n % 3 == 0 is true if either of the conditions is true,
that is, if the number is divisible by 2 or divisible by 3. In this case, one, or the other, or
both of the parts has to be true for the result to be true.
Finally, the not operator negates a boolean expression, so not x > y
is true if x > y is false, that is, if x is less than or equal to
y.
In [1]: x = 5
In [1]: x > 0 and x < 10
In [1]: n = 25
In [1]: n % 2 == 0 or n % 3 == 0
Common Mistake!
There is a very common mistake that occurs when programmers try to write
boolean expressions. For example, what if we have a variable number and
we want to check to see if its value is 5,6, or 7. In words we might say:
“number equal to 5 or 6 or 7”. However, if we translate this into Python,
number == 5 or 6 or 7, it will not be correct. The or operator must
join the results of three equality checks. The correct way to write this is
number == 5 or number == 6 or number == 7. This may seem like a lot of
typing but it is absolutely necessary. You cannot take a shortcut.
Check your understanding
-
data-2-32: What is the correct Python expression for checking to see if a number stored in a variable x is between 0 and 5.
- (A) x > 0 and < 5
- Each comparison must be between exactly two values. In this case the right-hand expression < 5 lacks a value on its left.
- (B) 0 < x < 5
- This is tricky. Although most other programming languages do not allow this syntax, in Python, this syntax is allowed. However, you should not use it. Instead, make multiple comparisons by using and or or.
- (C) x > 0 or x < 5
- Although this is legal Python syntax, the expression is incorrect. It will evaluate to true for all numbers that are either greater than 0 or less than 5. Because all numbers are either greater than 0 or less than 5, this expression will always be True.
- (D) x > 0 and x < 5
- Yes, with an and keyword both expressions must be true so the number must be greater than 0 an less than 5 for this expression to be true.
2.1.6. Precedence of Operators¶
We have now added a number of additional operators to those we learned in the
previous chapters. It is important to understand how these operators relate to
the others with respect to operator precedence. Python will always evaluate the
arithmetic operators first (** is highest, then multiplication/division, then
addition/subtraction). Next comes the relational operators. Finally, the
logical operators are done last. This means that the expression x*5 >= 10 and
y-6 <= 20 will be evaluated so as to first perform the arithmetic and then
check the relationships. The and will be done last. Although many
programmers might place parenthesis around the two relational expressions, it is
not necessary.
The following table summarizes the operator precedence from highest to lowest. A complete table for the entire language can be found in the Python Documentation.
| Level | Category | Operators |
|---|---|---|
| 7(high) | exponent | ** |
| 6 | multiplication | *,/,//,% |
| 5 | addition | +,- |
| 4 | relational | ==,!=,<=,>=,>,< |
| 3 | logical | not |
| 2 | logical | and |
| 1(low) | logical | or |
Note
This workspace is provided for your convenience. You can use this activecode window to try out anything you like.
Check your understanding
-
data-2-33: Which of the following properly expresses the precedence of operators (using parentheses) in the following expression: 5*3 > 10 and 4+6==11
- (A) ((5*3) > 10) and ((4+6) == 11)
- Yes, * and + have higher precedence, followed by > and ==, and then the keyword "and"
- (B) (5*(3 > 10)) and (4 + (6 == 11))
- Arithmetic operators (*, +) have higher precedence than comparison operators (>, ==)
- (C) ((((5*3) > 10) and 4)+6) == 11
- This grouping assumes Python simply evaluates from left to right, which is incorrect. It follows the precedence listed in the table in this section.
- (D) ((5*3) > (10 and (4+6))) == 11
- This grouping assumes that "and" has a higher precedence than ==, which is not true.
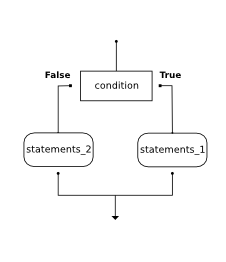
2.1.7. Conditional Execution: Binary Selection¶
In order to write useful programs, we almost always need the ability to check conditions and change the behavior of the program accordingly. The simplest form of selection is the if expression. This is sometimes referred to as binary selection since there are two possible paths of execution.
In [1]: x = 15
In [1]: "even" if x % 2 == 0 else "odd"
The syntax for an if expression looks like this:
EXPRESSION_1 if BOOLEAN EXPRESSION else EXPRESSION_2
The boolean expression after the if statement is called the condition.
If it is true, then the first expression is evaluated. If not, then the
expression after the else clause gets evaluated.
An important property of the conditional expression is that exactly one of the expressions is evaluated and not the other. This allows us to avoid errors that would otherwise be impossible to avoid, as illustrate by the following silly example.
In [1]: x = 15
In [1]: "No Error" if x == 15 else x / 0
If the conditional expression evaluated both expressions, then we would have encountered the following exception.
In [1]: 15 / 0
There is a limitation to the conditional expression. Since this is an expression, it can only contain values or other expressions. This means that we cannot include statements, such as the assignment statement in this expression. In a later section, we will introduce the if-elif-else statement to deal with this limitation.
In [1]: 3 if 5 == 4 else (x = 1)
Check your understanding
-
data-2-34: How many statements can appear in each expression (the if and the else) in a conditional expression?
- (A) Just one.
- The conditional expression may only consist of other expressions.
- (B) Zero or more.
- The conditional expression may only consist of other expressions.
- (C) One or more.
- The conditional expression may only consist of other expressions.
- (D) None.
- The conditional expression may only consist of other expressions.
- (A) True
- True is only evaluated if the conditional (in this case, 4+5 == 10) is true. In this case 5+4 is not equal to 10.
- (B) False
- Since 4+5==10 evaluates to False, Python will skip over the if expression and execute the expression after the else.
- (C) True on one line and False on the next
- Python would never evaluate both True and False because it will only evalutate one expression, but not both.
- (D) Nothing
- Python will always evaluate either the if-expression or the else-expression. It would never skip over both expressions.
data-2-35: What is the value of the following expression?
True if 4 + 5 == 10 else False