1.4. Sharing and Reusing Code with Modules — Runestone Interactive Overview

1.4.1. Modules and Getting Help¶

A module is a file containing Python definitions and statements intended for use in other Python programs. There are many Python modules that come with Python as part of the standard library.

The Python Documentation site for Python version 3 (the home page is shown below) is an extremely useful reference for all aspects of Python. The site contains a listing of all the standard modules that are available with Python (see Global Module Index). You will also see that there is a Language Reference and a Tutorial, as well as installation instructions, how-tos, and frequently asked questions. We encourage you to become familiar with this site and to use it often.

If you have not done so already, take a look at the Global Module Index. Here you will see an alphabetical listing of all the modules that are available as part of the standard library.

Note: Python modules and limitations with activecode

Throughout the chapters of this book, activecode windows allow you to practice the Python that you are learning. We mentioned in the first chapter that programming is normally done using some type of development environment and that the activecode used here was strictly to help us learn. It is not the way we write production programs.

To that end, it is necessary to mention that many of the modules available in standard Python will not work in the activecode environment. In fact, only turtle, math, and random have been ported at this point. If you wish to explore any additional modules, you will need to also explore using a more robust development environment.

Check your understanding

(A) A file containing Python definitions and statements intended for use in other Python programs.
A module can be reused in different programs.
(B) A separate block of code within a program.
While a module is separate block of code, it is separate from a program.
(C) One line of code in a program.
The call to a feature within a module may be one line of code, but modules are usually multiple lines of code separate from the program
(D) A file that contains documentation about functions in Python.
Each module has its own documentation, but the module itself is more than just documentation.

(A) Go to the Python Documentation site.
The site contains a listing of all the standard modules that are available with Python.
(B) Look at the import statements of the program you are working with or writing.
The import statements only tell you what modules are currently being used in the program, not how to use them or what they contain.
(C) Ask the professor
While the professor knows a subset of the modules available in Python, chances are the professor will have to look up the available modules just like you would.
(D) Look in this textbook.
This book only explains a portion of the modules available. For a full listing you should look elsewhere.

(A) True
Only turtle, math, and random have been ported to work in activecode at this time.
(B) False
Only turtle, math, and random have been ported to work in activecode at this time.

1.4.2. The math module¶

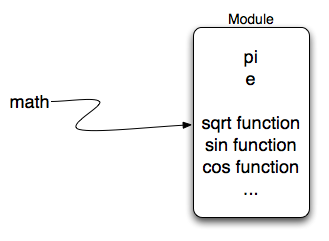
The math module contains the kinds of mathematical functions you would typically find on your calculator and some mathematical constants like pi and e. As we noted above, when we import math, we create a reference to a module object that contains these elements.

Here are some items from the math module in action. If you want more information, you can check out the Math Module Python Documentation.

Mathematical functions do not need to be constructed. They simply perform a task. They are all housed together in a module called math. Once we have imported the math module, anything defined there can be used in our program. Notice that we always use the name of the module followed by a dot followed by the specific item from the module (math.sqrt). You can think of this as lastname.firstname where the lastname is the module family and the firstname is the individual entry in the module.

If you have not done so already, take a look at the documentation for the math module.

Check your understanding

(A) import math
The module must be imported before you can use anything declared inside the module.
(B) include math
The correct term is not include, but you are close.
(C) use math
You will be using parts of the module, but that is not the right term.
(D) You don't need a statement. You can always use the math module
You cannot use a Python module without a statement at the top of your program that explicitly tells Python you want to use the module.

1.4.3. The `import` statement¶

There are three ways to import a module. The first is the basic import statement, as shown below.

In [1]: import math

When using this import statement, all the objects from the math module live in the math namespace and are accessed using the . notation. For example, to see an approximation of \(\pi\), we would use math.pi.

In [1]: math.pi

It can be inconvenient to type the module name before each object and there are two ways to avoid this annoyance. First, we could assign a short alias for the module using the import-as statement.

In [1]: import math as m

In [1]: m.cos(m.pi/2)

The other alternative is to import elements into the main namespace using the from-import statement, as shown below. In this case, we no longer need to use the module name and dot notation to access the objects.

In [1]: from math import pi, cos

In [1]: cos(pi/2)

You may be wondering why anyone might use the import or import-as statements and subject themselves to the inconvenience of prepending all module objects with the dot notation. The primary advantage to using these forms of the import statement is that they avoid naming conflicts. For example, both the math standard library and the numpy numerical library have a cosine function. In the example shown below, the second import statement shadows the first cos function from the math module, which usually leads to a bug.

In [1]: from math import pi, cos

In [1]: from numpy import cos

In [1]: cos(pi/2)

In this case, we were lucky that both cos functions worked the same way. The numpy cos function has the added functionality of working on lists. Let’s change the example to introduce a bug.

In [1]: from numpy import cos

In [1]: from math import pi, cos

In [1]: xs = [1,2,3]

In [1]: cos(xs)

In this last example, the math cos function “overwrites” the numpy cos because math is imported second. When trying to apply the cos to a list, we get an error as the math cos doesn’t work on a list, only numbers. We can avoid this shadowing using an alias for the modules.

In [1]: import numpy as np

In [1]: import math as m

In [1]: xs = [1,2,3]

In [1]: np.cos(xs)

1.4.4. The random module¶

We often want to use random numbers in programs. Here are a few typical uses:

To play a game of chance where the computer needs to throw some dice, pick a number, or flip a coin,
To shuffle a deck of playing cards randomly,
To randomly allow a new enemy spaceship to appear and shoot at you,
To simulate possible rainfall when we make a computerized model for estimating the environmental impact of building a dam,
For encrypting your banking session on the Internet.

Python provides a module random that helps with tasks like this. You can take a look at it in the documentation. Here are the key things we can do with it.

Press the run button a number of times. Note that the values change each time. These are random numbers.

The randrange function generates an integer between its lower and upper argument, using the same semantics as range — so the lower bound is included, but the upper bound is excluded. All the values have an equal probability of occurring (i.e. the results are uniformly distributed).

The random() function returns a floating point number in the range [0.0, 1.0) — the square bracket means “closed interval on the left” and the round parenthesis means “open interval on the right”. In other words, 0.0 is possible, but all returned numbers will be strictly less than 1.0. It is usual to scale the results after calling this method, to get them into a range suitable for your application.

In the case shown here, we’ve converted the result of the method call to a number in the range [0.0, 5.0). Once more, these are uniformly distributed numbers — numbers close to 0 are just as likely to occur as numbers close to 0.5, or numbers close to 1.0. If you continue to press the run button you will see random values between 0.0 and up to but not including 5.0.

It is important to note that random number generators are based on a deterministic algorithm — repeatable and predictable. So they’re called pseudo-random generators — they are not genuinely random. They start with a seed value. Each time you ask for another random number, you’ll get one based on the current seed attribute, and the state of the seed (which is one of the attributes of the generator) will be updated. The good news is that each time you run your program, the seed value is likely to be different meaning that even though the random numbers are being created algorithmically, you will likely get random behavior each time you execute.

Lab

Sine Wave In this guided lab exercise we will have the turtle plot a sine wave.

Check your understanding

(A) math.pi
To invoke or reference something contained in a module you use the dot (.) notation.
(B) math(pi)
This is the syntax for calling a function, not referencing an item in a module.
(C) pi.math
The module name must come first when accessing values and functions with a module.
(D) math->pi
The -> notation is not used in Python.

(A) the math module
While you might want to use the math module for other numerical computations in your program, it does not contain functions that are likely to help you simulate a dice roll.
(B) the random module
You would likely call the function random.randrange.
(C) the turtle module
The turtle module, while producing interesting graphics, is unlikely to help you here.
(D) the game module
Python does not have a game module.

(A) prob = random.randrange(1, 101)
This will generate a number between 1 and 101, but does not include 101.
(B) prob = random.randrange(1, 100)
This will generate a number between 1 and 100, but does not include 100. The highest value generated will be 99.
(C) prob = random.randrange(0, 101)
This will generate a number between 0 and 100. The lowest value generated is 0. The highest value generated will be 100.
(D) prob = random.randrange(0, 100)
This will generate a number between 0 and 100, but does not include 100. The lowest value generated is 0 and the highest value generated will be 99.

(A) There is no computer on the stage for the drawing.
They could easily put one there.
(B) Because computers don't really generate random numbers, they generate pseudo-random numbers.
Computers generate random numbers using a deterministic algorithm. This means that if anyone ever found out the algorithm they could accurately predict the next value to be generated and would always win the lottery.
(C) They would just generate the same numbers over and over again.
This might happen if the same seed value was used over and over again, but they could make sure this was not the case.
(D) The computer can't tell what values were already selected, so it might generate all 5's instead of 5 unique numbers.
While a programmer would need to ensure the computer did not select the same number more than once, it is easy to ensure this.

Note

This workspace is provided for your convenience. You can use this activecode window to try out anything you like.

1.4.5. Making your own modules¶

Making your own modules is as easy as saving the functions and values in a file with the .py extension. Provided that Python can find your file, you will now be able to import and use your code in other programs.

Note

The easiest way to make sure that Python can locate your module is keeping in in the current working directory. In IPython, you can see the location of the current working directory using the pwd magic alias.

In [1]: pwd

Other methods for providing access to your module includes adding the modules address to the PYTHONPATH or using the distutils standard module to provide an installation of your module. The best way to share a module in Python is using the Python Package Index, which allows users to install your program using pip. For more information, take a look at this tutorial.

1.4. Sharing and Reusing Code with Modules¶

1.4.1. Modules and Getting Help¶

1.4.2. The math module¶

1.4.3. The import statement¶

1.4.4. The random module¶

1.4.5. Making your own modules¶

1.4.3. The `import` statement¶