2.5. ExercisesΒΆ

  1. Add parenthesis to the expression 6 * 1 - 2 to change its value from 4 to -6.

  1. What is the order of the arithmetic operations in the following expression. Evaluate the expression by hand and then check your work.

    2 + (3 - 1) * 10 / 5 * (2 + 3)

  1. Many people keep time using a 24 hour clock (11 is 11am and 23 is 11pm, 0 is midnight). If it is currently 13 and you set your alarm to go off in 50 hours, it will be 15 (3pm). Write a Python program to solve the general version of the above problem using variables and lambda expressions. Print the solution to the specific example given above (i.e. current time is 13 and alarm goes off 50 hours later.)

  1. It is possible to name the days 0 through 6 where day 0 is Sunday and day 6 is Saturday. If you go on a wonderful holiday leaving on day number 3 (a Wednesday) and you return home after 10 nights. Write a general version of the program using variables and lambda expressions that takes the starting day number, and the length of your stay, and it will return the number of day of the week you will return on. Print the solution to the specific example of this problem presented above (i.e. leave on day 3 and return 10 nights later).

  1. Write a program that will compute the area of a rectangle. Use variable and lambda expressions in your solution. Solve an specific example and print a nice message with the answer.

  1. Write a program that will compute the area of a circle. Use variable and lambda expressions in your solution. Solve an specific example and print a nice message with the answer.

  1. Write a program that will convert degrees celsius to degrees fahrenheit.

  1. Write a program that will convert degrees fahrenheit to degrees celsius.

  1. Write a program that will compute MPG for a car. Use variable and lambda expressions in your solution. Solve an specific example and print a nice message with the answer.

  1. The formula for computing the final amount if one is earning compound interest is given on Wikipedia as

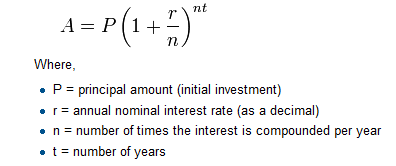
    formula for compound interest

    Write each of the following lambda expressions.

    1. Write a lambda expression named interest_multiplier that takes the interest rate r (integer) and the number of compound periods per year n and computes the one plus the decimal of the interest rate, i.e. \(1 + \frac{r}{n}\).
    2. Write a lambda expression named compound_interest_rate that takes r, n, and t as input and returns the compound interest rate multiplier for this given situation, i.e. \(\left(1 + \frac{r}{n} \right)^{n*t}\). Be sure to use your function from part 1 in your solution.
    3. Write a lambda expression named future_value that takes P, r, n, and t as input and returns the compound interest rate multiplier for this given situation, i.e. \(P*\left(1 + \frac{r}{n} \right)^{n*t}\). Be sure to use your functions from part 1 and 2 in your solution.

    Write a Python program that assigns the principal amount of 10000 to variable P, assign to n the value 12, and assign to r the interest rate of 8% (0.08), and a time t of 10 years. Calculate and print the final amount.

Next Section - 3. Sequential Data Structures in Python