In Python, a function is a named sequence of statements that belong together. Their primary purpose is to help us organize programs into chunks that match how we think about the solution to the problem. Thus far, we have defined our function using expressions and lambdas, but as functions becomes more complicated, we will want to use the function definition statement to make the function definition more readable.

The syntax for a function definition statement is:

def name( parameters ):
    statements

In a function definition, the keyword in the header is def, which is followed by the name of the function and some parameters enclosed in parentheses. The parameter list may be empty, or it may contain any number of parameters separated from one another by commas. In either case, the parentheses are required.

You can make up any names you want for the functions you create, except that you can’t use a name that is a Python keyword, and the names must follow the rules for legal identifiers that were given previously.

One of the primary distinctions between the function definition statement and lambda expressions is that functions defined with this statement will almost exclusively consist of statements. There can be any number of statements inside the function, but they have to be indented from the def. In the examples in this book, we will use the standard indentation of four spaces. Function definitions are and example of compound statements we will see, all of which have the same pattern:

A header line which begins with a keyword and ends with a colon.
A body consisting of one or more Python statements, each indented the same amount – 4 spaces is the Python standard – from the header line.

In functional programs the body of a function will mostly consist of assignment statements and possible an if-elif-else or try-except block. As we have seen, most iteration can be handled by a list comprehension and we in this chapter we will an additional alternative for loops in the form of recursion. The most important part of a fruitful function is the return statement the halts the function and returns one or more values.

Check your understanding

(A) A named sequence of statements.
Yes, a function is a named sequence of statements.
(B) Any sequence of statements.
While functions contain sequences of statements, not all sequences of statements are considered functions.
(C) A mathematical expression that calculates a value.
While some functions do calculate values, the python idea of a function is slightly different from the mathematical idea of a function in that not all functions calculate values. Consider, for example, the turtle functions in this section. They made the turtle draw a specific shape, rather than calculating a value.
(D) A statement of the form x = 5 + 4.
This statement is called an assignment statement. It assigns the value on the right (9), to the name on the left (x).

(A) To improve the speed of execution
Functions have little effect on how fast the program runs.
(B) To help the programmer organize programs into chunks that match how they think about the solution to the problem.
While functions are not required, they help the programmer better think about the solution by organizing pieces of the solution into logical chunks that can be reused.
(C) All Python programs must be written using functions
In the first several chapters, you have seen many examples of Python programs written without the use of functions. While writing and using functions is desirable and essential for good programming style as your programs get longer, it is not required.
(D) To calculate values.
Not all functions calculate values.

(A) def drawCircle(t):
A function may take zero or more parameters. It does not have to have two. In this case the size of the circle might be specified in the body of the function.
(B) def drawCircle:
A function needs to specify its parameters in its header.
(C) drawCircle(t, sz):
A function definition needs to include the keyword def.
(D) def drawCircle(t, sz)
A function definition header must end in a colon (:).

exceptions-4-24: What are the parameters of the following function?

def drawSquare(t, sz):
    """Make turtle t draw a square of with side sz."""
    for i in range(4):
        t.forward(sz)
        t.left(90)

(A) i
i is a variable used inside of the function, but not a parameter, which is passed in to the function.
(B) t
t is only one of the parameters to this function.
(C) t, sz
Yes, the function specifies two parameters: t and sz.
(D) t, sz, i
the parameters include only those variables whose values that the function expects to receive as input. They are specified in the header of the function.

exceptions-4-25: Considering the function below, which of the following statements correctly invokes, or calls, this function (i.e., causes it to run)? Assume we already have a turtle named alex.

def drawSquare(t, sz):
    """Make turtle t draw a square of with side sz."""
    for i in range(4):
        t.forward(sz)
        t.left(90)

(A) def drawSquare(t, sz)
No, t and sz are the names of the formal parameters to this function. When the function is called, it requires actual values to be passed in.
(B) drawSquare
A function call always requires parentheses after the name of the function.
(C) drawSquare(10)
This function takes two parameters (arguments)
(D) drawSquare(alex, 10):
A colon is only required in a function definition. It will cause an error with a function call.
(E) drawSquare(alex, 10)
Since alex was already previously defined and 10 is a value, we have passed in two correct values for this function.

Functions¶

When writing functional programs, we focus on functions that return values, called fruitful functions. In many other languages, a chunk that doesn’t return a value is called a procedure, which we will call non-fruitful. It is worth noting that non-fruitful functions will almost always be side-effecting (what else could they do?). Understanding a program that uses side-effecting functions can be difficult, because the nature of the side-effect is not obvious in the function call. Consequently, functional programs involve writing pure fruitful functions whenever possible. A pure function is a side-effect free fruitful function, making it referentially transparent.

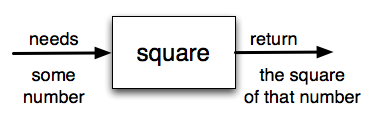
How do we write our own fruitful function? Let’s start by creating a very simple mathematical function that we will call square. The square function will take one number as a parameter and return the result of squaring that number. Here is the black-box diagram with the Python code following.

In [1]: def square(x):
   ...:     """ Return the square of the number x"""
   ...:     y = x * x
   ...:     return y
   ...: 

In [1]: number = 10

In [1]: result = square(number)

In [1]: result

The return statement is followed by an expression which is evaluated. Its result is returned to the caller as the “fruit” of calling this function. Because the return statement can contain any Python expression we could have avoided creating the temporary variable y and simply used return x*x. On the other hand, using temporary variables like y in the program above makes the code easier to read and debug. Temporary variables assigned inside the body of a function are local variables and have a scope that includes the body of the functions.

docstrings

If the first thing after the function header is a string (some tools insist that it must be a triple-quoted string), it is called a docstring and gets special treatment in Python and in some of the programming tools.

Another way to retrieve this information is to use the interactive interpreter, and enter the expression <function_name>.__doc__, which will retrieve the docstring for the function. So the string you write as documentation at the start of a function is retrievable by python tools at runtime. This is different from comments in your code, which are completely eliminated when the program is parsed.

By convention, Python programmers use docstrings for the key documentation of their functions.

As with lambda expressions, defining a new function does not make the function run. To do that we need a function call using the same syntax as used with built-in functions and lambda expressions.

Notice something important here. The name of the variable we pass as an argument — number — has nothing to do with the name of the formal parameter — x. It is as if x = toSquare is executed when square is called. It doesn’t matter what the value was named in the caller. In square, it’s name is x. You can see this very clearly in codelens, where the global variables and the local variables for the square function are in separate boxes.

As you step through the example in codelens notice that the return statement not only causes the function to return a value, but it also returns the flow of control back to the place in the program where the function call was made.

(ch04_clsquare)

Another important thing to notice as you step through this codelens demonstration is the movement of the red and green arrows. Codelens uses these arrows to show you where it is currently executing. Recall that the red arrow always points to the next line of code that will be executed. The light green arrow points to the line that was just executed in the last step.

When you first start running this codelens demonstration you will notice that there is only a red arrow and it points to line 1. This is because line 1 is the next line to be executed and since it is the first line, there is no previously executed line of code.

When you click on the forward button, notice that the red arrow moves to line 5, skipping lines 2 and 3 of the function (and the light green arrow has now appeared on line 1). Why is this? The answer is that function definition is not the same as function execution. Lines 2 and 3 will not be executed until the function is called on line 6. Line 1 defines the function and the name square is added to the global variables, but that is all the def does at that point. The body of the function will be executed later. Continue to click the forward button to see how the flow of control moves from the call, back up to the body of the function, and then finally back to line 7, after the function has returned its value and the value has been assigned to squareResult.

Finally, there is one more aspect of function return values that should be noted. All Python functions return the value None unless there is an explicit return statement with a value other than None. Consider the following common mistake made by beginning Python programmers. As you step through this example, pay very close attention to the return value in the local variables listing. Then look at what is printed when the function returns.

(ch04_clsquare_bad)

The problem with this function is that even though it prints the value of the square, that value will not be returned to the place where the call was done. Since line 6 uses the return value as the right hand side of an assignment statement, the evaluation of the function will be None. In this case, squareResult will refer to that value after the assignment statement and therefore the result printed in line 7 is incorrect. Typically, functions will return values that can be printed or processed in some other way by the caller.

Occasionally, we will also need to write non-fruitful functions, which are also sometimes referred to as procedures or void functions. The figure below illustrates the black-box diagram of a void function. These values, often called arguments or actual parameters, are passed to the function by the user.

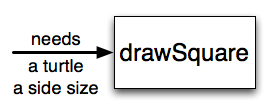
Suppose we’re working with turtles and a common operation we need is to draw squares. It would make sense if we did not have to duplicate all the steps each time we want to make a square. “Draw a square” can be thought of as an abstraction of a number of smaller steps. We will need to provide two pieces of information for the function to do its work: a turtle to do the drawing and a size for the side of the square. We could represent this using the following black-box diagram.

Here is a program containing a function to capture this idea. Give it a try.

Everything that this function does is a side-effect. The import statement adds the turtle library to the main name space (a side-effect). The function definition save the associated function value to the main namespace (a side-effect). The turtle.Screen call makes an external screen for turtles (a side-effect)... etc. All programs need some part of their code to be side-effecting, if nothing else we need to read data in and output results. The goals in functional programming, regarding side-effect are as follows.

Make as many functions as possible pure and fruitful. We will test these functions to confirm that they are correct and once tested, we will know that they are not the source of any bugs in our program.
Write small functions and provide a quality name for each. Each function should perform one and only one abstract task.
Refactor longer functions by identifying portions of the code that perform some task and putting this code in another function.

Always be aware of side-effects and try to capture and contain side-effects in a small number of functions. Side-effecting functions are much hard to test, which is one of the reasons that we will keep them to a minimum.

We will dedicate more time to each of these topics in the upcoming sections.

Check your understanding

exceptions-4-26: What is wrong with the following function definition:

def addEm(x, y, z):
    return x + y + z
    print('the answer is', x + y + z)

(A) You should never use a print statement in a function definition.
Although you should not mistake print for return, you may include print statements inside your functions.
(B) You should not have any statements in a function after the return statement. Once the function gets to the return statement it will immediately stop executing the function.
This is a very common mistake so be sure to watch out for it when you write your code!
(C) You must calculate the value of x+y+z before you return it.
Python will automatically calculate the value x+y+z and then return it in the statement as it is written
(D) A function cannot return a number.
Functions can return any legal data, including (but not limited to) numbers, strings, turtles, etc.

exceptions-4-27: What will the following function return?

def addEm(x, y, z):
    print(x + y + z)

(A) Nothing (no value)
We have accidentally used print where we mean return. Therefore, the function will return the value None by default. This is a VERY COMMON mistake so watch out! This mistake is also particularly difficult to find because when you run the function the output looks the same. It is not until you try to assign its value to a variable that you can notice a difference.
(B) The value of x + y + z
Careful! This is a very common mistake. Here we have printed the value x+y+z but we have not returned it. To return a value we MUST use the return keyword.
(C) The string 'x + y + z'
x+y+z calculates a number (assuming x+y+z are numbers) which represents the sum of the values x, y and z.

Program Development¶

At this point, you should be able to look at complete functions and tell what they do. Also, if you have been doing the exercises, you have written some small functions. As you write larger functions, you might start to have more difficulty, especially with runtime and semantic errors.

To deal with increasingly complex programs, we are going to suggest a technique called incremental development. The goal of incremental development is to avoid long debugging sessions by adding and testing only a small amount of code at a time.

As an example, suppose you want to find the distance between two points, given by the coordinates (x₁, y₁) and (x₂, y₂). By the Pythagorean theorem, the distance is:

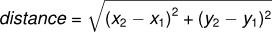
The first step is to consider what a distance function should look like in Python. In other words, what are the inputs (parameters) and what is the output (return value)?

In this case, the two points are the inputs, which we can represent using four parameters. The return value is the distance, which is a floating-point value.

Already we can write an outline of the function that captures our thinking so far.

def distance(x1, y1, x2, y2):
    return 0.0

Obviously, this version of the function doesn’t compute distances; it always returns zero. But it is syntactically correct, and it will run, which means that we can test it before we make it more complicated.

To test the new function, we call it with sample values.

We chose these values so that the horizontal distance equals 3 and the vertical distance equals 4; that way, the result is 5 (the hypotenuse of a 3-4-5 triangle). When testing a function, it is useful to know the right answer.

At this point we have confirmed that the function is syntactically correct, and we can start adding lines of code. After each incremental change, we test the function again. If an error occurs at any point, we know where it must be — in the last line we added.

A logical first step in the computation is to find the differences x₂- x₁ and y₂- y₁. We will store those values in temporary variables named dx and dy.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    return 0.0

Next we compute the sum of squares of dx and dy.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquared = dx**2 + dy**2
    return 0.0

Again, we could run the program at this stage and check the value of dsquared (which should be 25).

Finally, using the fractional exponent 0.5 to find the square root, we compute and return the result.

If that works correctly, you are done. Otherwise, you might want to print the value of result before the return statement.

When you start out, you might add only a line or two of code at a time. As you gain more experience, you might find yourself writing and debugging bigger conceptual chunks. As you improve your programming skills you should find yourself managing bigger and bigger chunks: this is very similar to the way we learned to read letters, syllables, words, phrases, sentences, paragraphs, etc., or the way we learn to chunk music — from indvidual notes to chords, bars, phrases, and so on.

The key aspects of the process are:

Start with a working skeleton program and make small incremental changes. At any point, if there is an error, you will know exactly where it is.
Use temporary variables to hold intermediate values so that you can easily inspect and check them.
Once the program is working, you might want to consolidate multiple statements into compound expressions, but only do this if it does not make the program more difficult to read.