5.4. Computational Complexity¶

Dictionaries are designed to efficiently look up the value for a given key. This is accomplished by storing the data in a sorted, balanced binary tree. First, the hash value of a key is determined using the hash function. This function assigns a unique integer to each key and is used to sort the keys. The keys are then stored in the tree using a clever sorting scheme.

To mock up this process, let’s start with some keys and values that we want to store for fast look-up.

In [1]: keys = ['a', 'b', 'c', 'd', 'e', 'm', 'n']

In [2]: values = [1, 2, 3, 4, 5, 6, 7]

Next, we find the associated hash values. We want to associate these three values (hash, key, value), which is easy to do with zip.

In [3]: key_hashes = [hash(key) for key in keys]

In [4]: key_hashes
Out[4]: 
[-2755768832532532667,
 -2733652328786143893,
 -7361821637513938770,
 -3819602847015949274,
 -6904592001573243786,
 2612521463512525672,
 3255573614260948802]

In [5]: triples = list(zip(key_hashes, keys, values))

In [6]: triples
Out[6]: 
[(-2755768832532532667, 'a', 1),
 (-2733652328786143893, 'b', 2),
 (-7361821637513938770, 'c', 3),
 (-3819602847015949274, 'd', 4),
 (-6904592001573243786, 'e', 5),
 (2612521463512525672, 'm', 6),
 (3255573614260948802, 'n', 7)]

Before we can efficiently put these value in a search tree, we must sort these triples by the hash values.

In [7]: from toolz import get

In [8]: get_hash = lambda triple: get(0, triple)

In [9]: sorted_triples = sorted(triples, key=get_hash)

In [10]: sorted_triples
Out[10]: 
[(-7361821637513938770, 'c', 3),
 (-6904592001573243786, 'e', 5),
 (-3819602847015949274, 'd', 4),
 (-2755768832532532667, 'a', 1),
 (-2733652328786143893, 'b', 2),
 (2612521463512525672, 'm', 6),
 (3255573614260948802, 'n', 7)]

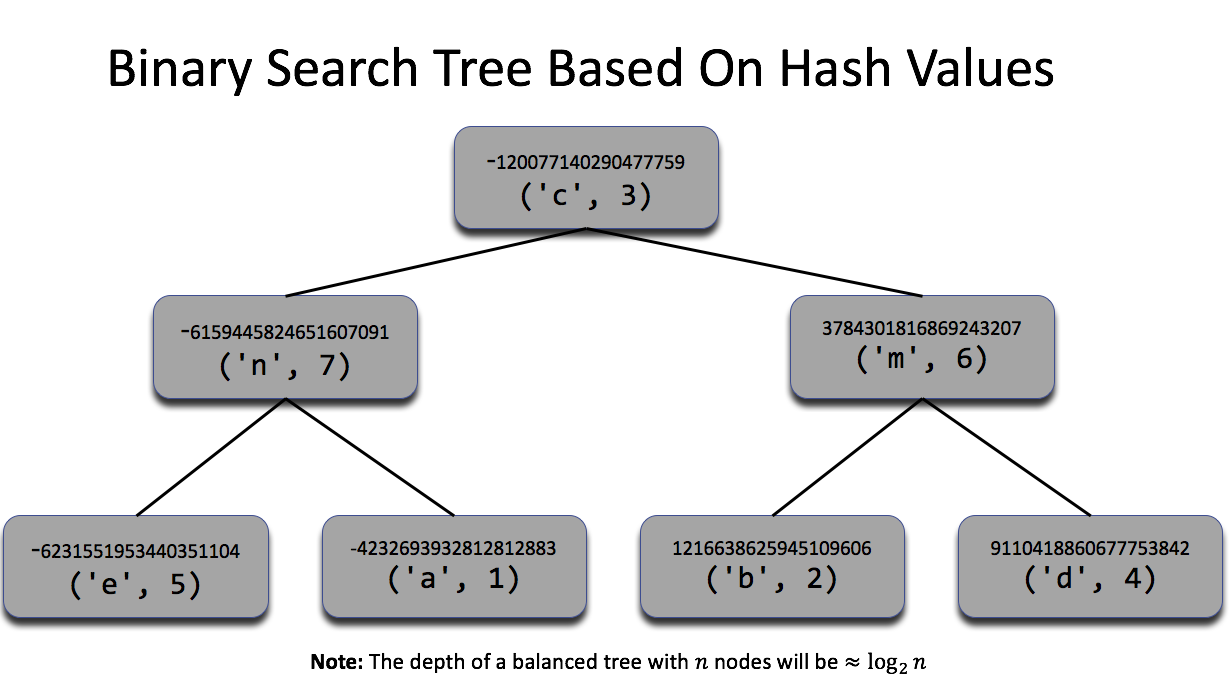
Now we place the triples in a search tree with the following strategy:

• All triples below and to the left the current node have a smaller hash than the current node.
• All triples below and to the right the current node have a larger hash than the current node.

The following figure illustrates the tree for this example (with the has values shortened to save space).

This diagram illustrates a balanced binary search tree based on the hash value of a key. The tree has the property that, for every node, all nodes below and to the left have smaller hash values and all nodes below and to the right have larger hash values. Note that the depth of a balanced binary search tree with \(n\) nodes will be approximately \(\log_2(n)\).

If, after constructing the tree, we needed to look up the value for 'b'. We would first compute the hash value for 'b' and then start our search at the top of the tree. The hash value for 'b' is larger than that of 'c'', so we proceed down the tree to the right. Next, the hash value of 'b' is compared to that of 'm'. This time the has value of 'b' is smaller, so we head down the tree to the left. Finally, we compare the hash value of 'b' to the hash value of the current node and find that it is the same. Consequently, the value on this node, 2, is returned. This search process is illustrated in the next figure.

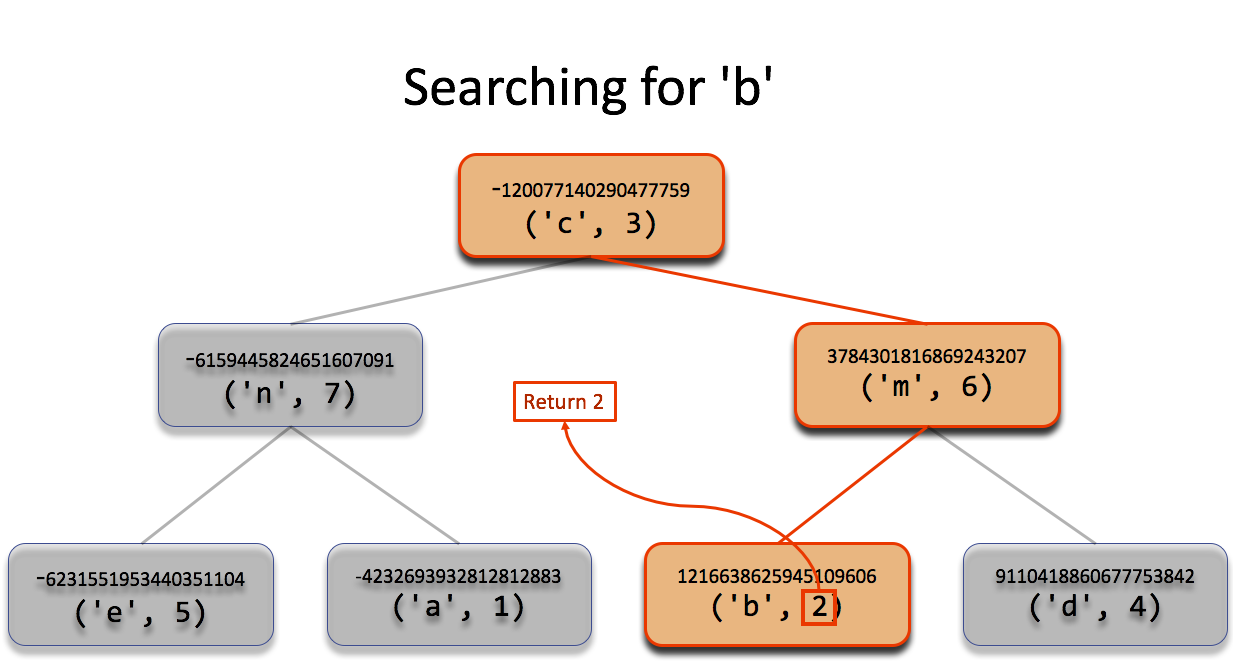
When searching the tree, the hash value of 'b' is compared to the hash value of each node, starting at the top of the tree. In this case, our hash value is larger than the first (head right), smaller than the second (head left) and the same as the third (return the value).

Another example of a search, this time for 'n' is pictured below. This time the hash value was smaller than the top node (head left) and the same as the second node (return the value).

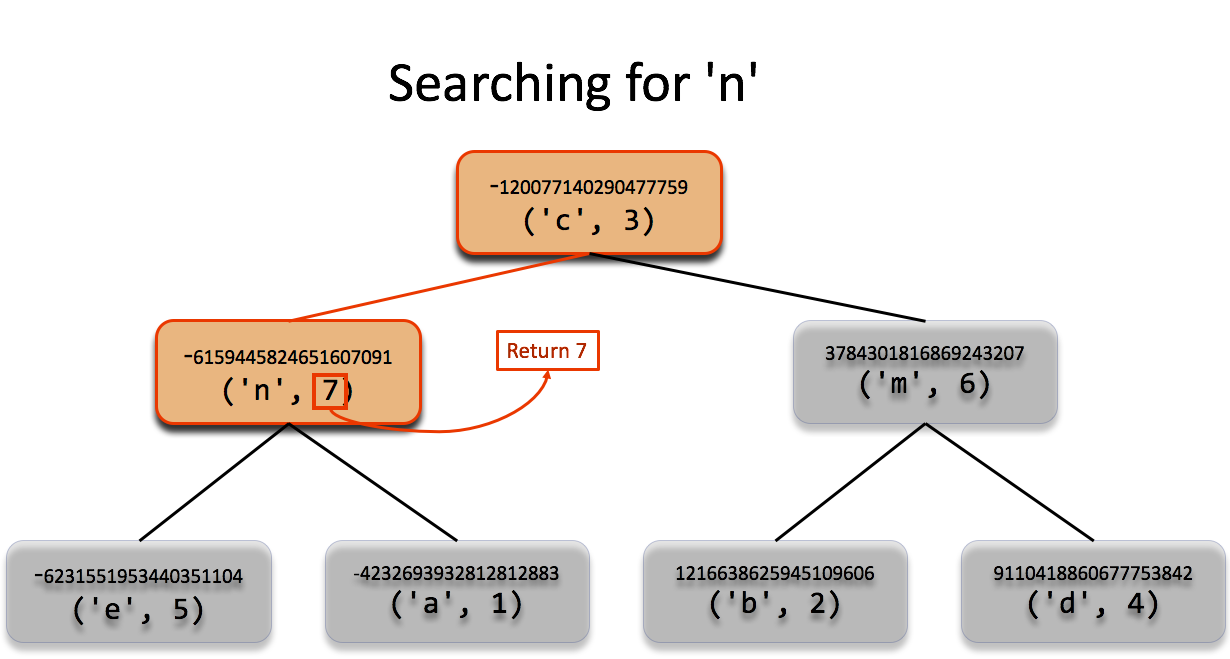
This diagram illustrates the search for 'n'. In this case, the hash value of 'n' is smaller than that of 'c' (head left) and the same as the hash on the second node. Consequently the the value of the second node, 7, is returned.

Because the tree depth for a balanced tree is approximately \(\log_2(n)\) for a tree containing \(n\) values, the time complexity of looking up values in a dictionary has time complexity of \(O(\log_2(n))\). The time complexity of checking for the presence of a key in a dictionary or an item in a set is also \(O(\log_2(n))\).

If you compare these complexities to that of a look-up for a list or tuple, which was \(O(n)\), we see that look-ups are much more efficient for sets and dictionaries!